
Start Sieci jednokierunkowe Sieci rekurencyjne Słowniczek Linki O autorach
Wybór struktury sieci neuronowej
Jednym zdaniem...
... jest to pierwszy problem, przed którym staje projektant sieci.
Zobaczyć działanie neuronu
Na wstępie małe wyjaśnienie: przy wyborze struktury sieci przede wszystkim należy ustalić, czy będzie to sieć jednokierunkowa, czy rekurencyjna. Przyjąłem, że to jest już ustalone - uczymy się o sieciach jednokierunkowych, ich zatem używamy. W drugiej części wykładów mój kolega zajmie się sieciami rekurencyjnymi. Zaznaczę tylko, że sieci rekurencyjne bardziej niż jednokierunkowe nadają się do problemów typu optymalizacja, czy asocjacja - więcej o tym w części "dla fachowców".
Wróćmy do tematu: co to znaczy "zobaczyć działanie neuronu"? Rozważmy neuron nieliniowy o dwóch wejściach. Powiedzmy, że na wejścia możemy podawać liczby w zakresie od -6 do 6. Wyjście, jak wiadomo, może przyjmować wartość -1 lub 1. Każda kombinacja wejść będzie miała "swoją" wartość wyjścia. Wyobraź sobie układ współrzędnych, w którym X i Y to wejścia neuronu. Każda kombinacja wartości wejść wyznacza w tym układzie współrzędnych punkt (dla wejść: 2, 4 będzie to punkt o współrzędnych (2, 4)). Oznaczmy go kolorem: niebieskim, jeśli dla tych wartości wejść odpowiedź neuronu jest pozytywna (1), lub czerwonym, jeśli odpowiedź jest negatywna (-1). Jeśli chcesz sam popróbować, użyj poniższego appletu. Symuluje on działanie jednego nieliniowego neuronu (umówmy się, że dalej będziemy przyjmować automatycznie, że neuron jest nieliniowy; jeśli będzie liniowy, wtedy to zaznaczę). Jego wagi są już ustalone (ale możesz je zmienić). Możesz podać wartości wejść, by zobaczyć ich reprezentację jako punkt w układzie współrzędnych - punkt o kolorze zależnym od odpowiedzi neuronu na te wejścia. Możesz także zlecić appletowi umieszczenie na wykresie pewnej liczby losowo wybranych punktów (nie więcej niż 10000 na raz). Jeśli w czasie testowania neuronu zmienisz jedną z wag, wszystkie punkty znikną i zaczniesz eksperymentować na nowo (neuron o innych wagach jest już bowiem całkiem innym neuronem). Postaraj się z grubsza wypełnić punktami cały układ współrzędnych. Powinieneś zaobserwować coś ciekawego.
Jak widzisz, perceptron tworzy w przestrzeni wejść linię prostą, która dzieli ową przestrzeń na dwa obszary. W jednym z nich są punkty reprezentujące obiekty akceptowane przez neuron, w drugim zaś - odrzucane. Jakie to ma konsekwencje? Ano takie, że sieć jednowarstwowa (w przykładzie zastosowałem pojedynczy neuron, ale jednowarstwowa sieć zachowuje się identycznie) może rozwiązywać tylko zadania liniowo separowalne. A po ludzku: jeśli wybierzemy sobie obiekty, które sieć ma akceptować lub odrzucać, a następnie w układzie współrzędnych zaznaczymy odpowiadające im punkty, to musi istnieć taka linia prosta, która oddzieli wszystkie punkty "pozytywne" od "negatywnych". Porównaj te wykresy:
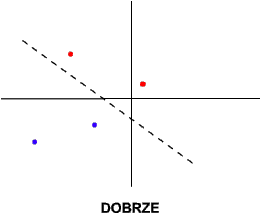
|
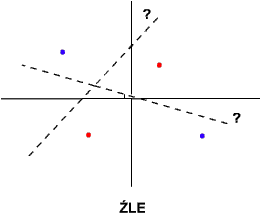
|
Taki wykres można narysować dla sieci o dwóch wejściach. Jeśli weźmiemy sieć o trzech wejściach, możemy się jeszcze pokusić o wizualizację trójwymiarowej przestrzeni wejść, gdzie każdy obiekt będzie reprezentowany przez punkt o trzech współrzędnych. Tu zamiast linii będzie musiała istnieć płaszczyzna oddzielająca punkty "pozytywne" od "negatywnych". Dla większej ilości wejść, kiedy nasza wyobraźnia odmawia pracy z więcej niż trzema wymiarami, trzeba posłużyć się matematyką. O tym jednak w części "dla fachowców".
Jeszcze tylko jedna dygresja: być może zwróciłeś uwagę na fakt, iż w powyższym applecie prosta wyznaczająca preferencje neuronu zawsze przebiega przez początek układu współrzędnych, czyli punkt (0, 0). Jest to pewne ograniczenie dla neuronu, ale wymyślono na nie sposób. Jest to tak zwany bias, który niech na razie pozostanie tajemnicą. Omówię go w pierwszym rozdziale części o uczeniu sieci.
Zaczynają się schody
Z powodu wymogu liniowej separowalności zadania dla sieci jednowarstwowej nie można za jej pomocą rozwiązać na przykład zadania XOR, czyli alternatywy wykluczającej. Działa ona podobnie, jak zwykła alternatywa (OR). Różnica polega na tym, że alternatywa dwóch zdań jest fałszem tylko w przypadku, kiedy oba zdania są fałszywe, zaś alternatywa wykluczająca - kiedy oba są fałszywe lub oba są prawdziwe. Dla jasności - tabelka:
| Zdanie A | Zdanie B | A OR B | A XOR B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 |
Spróbujmy rozwiązać zadanie XOR za pomocą sieci neuronowej. Będzie to sieć o dwóch wejściach (A i B) i jednym wyjściu (A XOR B). Przyjmijmy, że dla wyniku XOR równego 1 na wyjściu ma się pojawić sygnał akceptacji (1), a dla wyniku XOR równego 0 - sygnał odrzucenia (-1). Oznacza to, że po podaniu na wejście obiektu: (0, 1) sieć odpowie: 1 (0 XOR 1 = 1) i tak dalej. Zaznaczmy wszystkie możliwe obiekty wejściowe w układzie współrzędnych. Kolorem niebieskim oznaczę obiekty "pozytywne" (wyjście = 1), a kolorem czerwonym - negatywne (wyjście = -1).
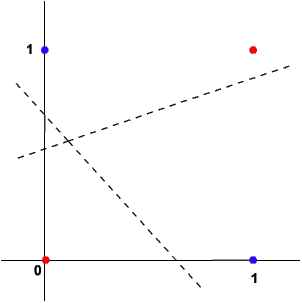
Nie da się oddzielić punktów czerwonych od niebieskich linią prostą (linie przerywane to nieudane próby), a co za tym idzie sieć jednokierunkowa jest bezsilna w konfrontacji z zadaniem XOR. Jeśli w poprzednim rozdziale w applecie symulującym sieć o pięciu wejściach próbowałeś nauczyć neurony rozpoznawania obiektów: (1, 1, 1, 1, 1), (2, 2, 2, 2, 2) oraz (3, 3, 3, 3, 3), to teraz już chyba rozumiesz, dlaczego zakończyło się to fiaskiem. Pięciowymiarowej przestrzeni nie potrafisz sobie wyobrazić, jednak możesz spróbować okroić tę sieć do dwóch wejść. Wówczas masz obiekty: (1, 1), (2, 2) i (3, 3). Drugi neuron miał rozpoznawać obiekt (2, 2), a odrzucać dwa pozostałe obiekty. Narysujmy wykres dla tej sytuacji:
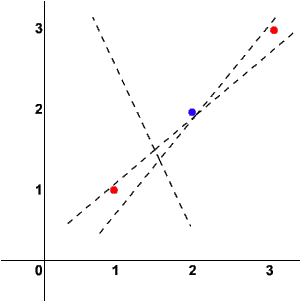
Chyba nie muszę tego komentować. Jeśli nie zrozumiałeś, przeczytaj jeszcze raz dokładnie ten (a może i poprzedni) rozdział.
Na wszystko jest sposób
Ubolewając nad niemożnością rozwiązania zadania XOR wciąż powtarzałem: "sieć jednowarstwowa". Domyśliłeś się już zapewne, iż aby ominąć te trudności należy użyć sieci wielowarstwowej. Powód tego zjawiska leży w sposobie, na który sieci wielowarstwowe dzielą przestrzeń wejść. Sieć dwuwarstwowa wyznacza w przestrzeni wejść wypukły i spójny obszar, w którym znajdują się punkty odpowiadające akceptowanym przez sieć obiektom wejściowym (czyli takim, które po podaniu na wejście wywołują odpowiedź równą 1). Oto dwa przykłady wizualizacji działania sieci dwuwarstwowej z zaznaczonymi na niebiesko obszarami pozytywnej odpowiedzi:
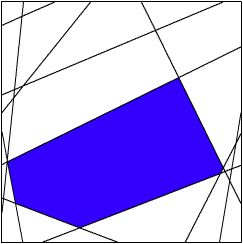
|
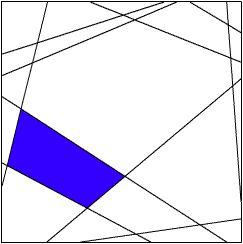
|
Ilość linii zależy od ilości neuronów w sieci. Jeśli weźmiesz jakikolwiek punkt z niebieskiego obszaru i podasz jego współrzędne na wejście danej sieci, odpowiedź będzie równa 1. Może zauważyłeś, że sieć dwuwarstwowa nie będzie miała problemów z zadaniem XOR:
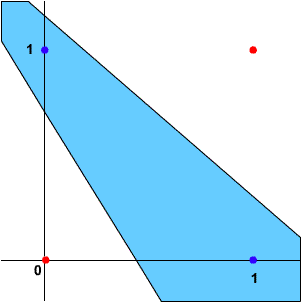
Na marginesie dodam, że przykład z funkcją XOR jest sztandarowym przykładem przerabianym na uczelni - z pewnością pojawi się na jednej z pierwszych wejściówek.
Co do sieci trzywarstwowej - wyznacza ona taki obszar pozytywnej odpowiedzi, który nie musi być ani spójny, ani wypukły. Może wyglądać tak, jak jeden z tych dwóch:

|
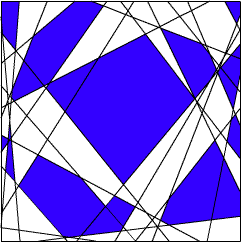
|
Jak widać, sieć trzywarstwowa jest w stanie rozwiązać praktycznie każdy rodzaj zadania. Dodam jeszcze, że takie różnice między sieciami o różnej liczbie warstw występują tylko w sieciach nieliniowych. Sieć liniowa zawsze, niezależnie od ilości warstw, dzieli obszar przestrzeń wejść linią prostą.
Wybieramy odpowiednią strukturę
Biorąc pod uwagę to, co powinieneś w tym momencie wiedzieć, zamieszczam ten podpunkt jedynie w celach kosmetycznych. Kiedy chcemy wykorzystać sieć w jakimś zadaniu, musimy je dokładnie przeanalizować. Im mniej warstw w sieci, tym szybciej i łatwiej zazwyczaj przebiega proces uczenia. Trzeba jednak wybrać taką sieć, która jest w stanie rozwiązać dany problem. Sieć jednowarstwowa problemu XOR nie rozwiąże - jest po prostu na to zbyt prymitywna. Nie można także przesadzić w drugą stronę - sieć nie powinna być zbyt inteligentna jak na swoje zadanie (a dlaczego - odpowiem w rozdziale o uczeniu sieci). Sieć trzywarstwowa może rozwiązać każdy rodzaj zadania, jednak czasem stosuje się sieci czterowarstwowe, aby uniknąć przymusu umieszczania zbyt wielu neuronów w jednej warstwie.
Wiesz już z grubsza, ile warstw powinna mieć Twoja sieć. Czas na bardziej szczegółowe określenie jej parametrów. W następnym rozdziale dowiesz się, jak efektywnie zagospodarować wejścia i wyjścia sieci.

Start Sieci jednokierunkowe Sieci rekurencyjne Słowniczek Linki O autorach