
Start Sieci jednokierunkowe Sieci rekurencyjne Słowniczek Linki O autorach
Jak używać sieci neuronowej
Jednym zdaniem...
... nie ma jednego określonego sposobu - wszystko zależy od rodzaju zadania.
Co na wejście?
To zależy od specyfiki zadania. W poprzednim rozdziale zajmowaliśmy się głównie klasyfikacją punktów w układzie współrzędnych. Stosowaliśmy dwa wejścia - każde na jedną współrzędną. To bodajże najprostszy przykład użycia wejść sieci. Przeważnie jednak mamy do czynienia z obiektami dużo bardziej skomplikowanymi i posiadającymi więcej cech, niż punkt. Wtedy trzeba trochę pokombinować.
Przede wszystkim musimy ocenić, które z cech obiektu będą dla niego reprezentatywne. To zależy od tego, pod jakim względem chcemy obiekty segregować. Jeśli na przykład chcemy zbudować sieć, która rozpoznaje różne modele gitar basowych (i tylko gitary basowe będą się pojawiać na wejściu), to darujemy sobie informowanie sieci o ilości strun gitary. Każda z nich ma bowiem cztery struny i pod tym względem się między sobą nie różnią. Musimy natomiast jakoś sieć powiadomić o wielkości gitary, kształcie pudła, długości gryfu i innych cechach różniących różne marki gitar. Liczbę strun podalibyśmy sieci, która miałaby klasyfikować wszystkie gitary, zarówno czterostrunowe, jak i sześciostrunowe. Dla takiej sieci liczba strun jest rzeczą niezmiernie ważną. Jak widać, to, czy dana cecha jest ważna, czy nie, jest silnie uzależnione od specyfiki zadania. Warto się poważnie zastanowić nad ilością cech podawanych sieci, gdyż dla każdej z nich musimy mieć osobne wejście.
W jaki sposób podawać wartości typu: wysokość, długość, itp.? W centymetrach? Raczej nie. Sieć operuje typowo ludzkim pojęciami. Zamiast podawać jej, że człowiek ma 145 cm wzrostu, trzeba jedynie dać jej do zrozumienia, że jest on niski. Pojęcia niskości i wysokości także są względne. To, jakiej skali tu użyjemy i na jakie wartości przełożymy odpowiednie cechy, zależy wyłącznie od nas. Możemy zrobić na przykład tak:
| Wzrost człowieka | Wartość którą podamy na wejście sieci |
| < 150 cm | 1 |
| 151 - 170 cm | 2 |
| > 170 cm | 3 |
Albo tak:
| Wzrost człowieka | Wartość którą podamy na wejście sieci |
| < 160 cm | 1 |
| 161 - 180 cm | 2 |
| > 180 cm | 3 |
I jeszcze inaczej:
| Wzrost człowieka | Wartość którą podamy na wejście sieci |
| < 140 cm | 1 |
| 141 - 150 cm | 2 |
| 151 - 170 cm | 3 |
| 171 - 180 cm | 4 |
| > 180 cm | 5 |
O ile w dwóch pierwszych tabelkach dzieliliśmy ludzi na niskich, średnich i wysokich, o tyle w trzeciej mamy już podział na bardzo niskich, niskich, średnich, wysokich i bardzo wysokich. Jest zatem dowolność w dobieraniu skali. Zależy, co komu potrzebne.
Inny nieco sposób podawania danych na wejście to podawanie sygnału dodatniego, jeśli obiekt daną cechę posiada, a ujemnego - jeśli jej nie posiada. Tak było dwa rozdziały temu w przykładzie z motoryzacyjnym neuronem. Jeśli obiekt jakąś cechę ma, dajemy na wejście 1. Jeśli on ją nawet "bardzo ma", dajemy 2 lub 3. Jeśli zaś jej nie ma, lub "bardzo nie ma", dajemy odpowiednio: -1, -2, lub -3.
Kolejny, całkiem odmienny sposób podawania danych na wejście sieci wykorzystuje się przy rozpoznawaniu obrazu. Przypuśćmy, że sieć ma rozpoznawać parę prostych znaków. Oto jeden z nich:
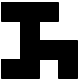
W jaki sposób podać go na wejście sieci? Podzielmy go na małe kwadraty:

Wyszło nam 16 kwadratów. Stwórzmy zatem sieć o 16 wejściach każde z nich przypiszmy jednemu z kwadratów, kolejno od lewego górnego rzędami w dół. Jeśli kwadrat jest wypełniony, podajemy na wejście 1, a jeśli pusty - 0. W naszym przypadku na kolejne wejścia podamy wartości: (spójrz na powyższy rysunek): (1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1). Pójdźmy dalej: jeśli niektóre pola pojaśnimy i otrzymamy rysunek "kolorowy", tak jak poniżej:
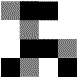
|

|
Wtedy możemy każdemu z wejść odpowiadającym jaśniejszym kwadratom nadać wartość 1/2. Ale szerzej o rozpoznawaniu obrazu opowie mój kolega Mariusz w części poświęconej sieciom rekurencyjnym.
Co na wyjściu?
Jeśli nasza sieć klasyfikuje obiekty na zasadzie: pasuje / nie pasuje, to wystarczy nam jedno wyjście. Jego wartość powie nam, czy dany obiekt został zaakceptowany (1: tak; -1: nie). W przykładzie z gitarami basowymi będziemy potrzebowali tylu neuronów w warstwie wyjściowej, ile modeli gitar ma dana sieć rozpoznawać. Każdemu wyjściu zostanie przyporządkowany model. Jedynka na tym wyjściu oznacza, że rozpoznawana gitara jest właśnie tej marki. Ale zastanówmy się, czy nie dało by się rozwiązać tego w lepszy sposób. Jeśli chcemy, by sieć rozpoznawała 15 modeli gitar, tworzymy 15 wyjść. Zauważ jednak, że nie będzie raczej sytuacji, w której jedynka będzie występować na więcej niż jednym wyjściu (gitara nie może być jednocześnie dwóch marek). Wygląda to zatem na marnotrawstwo. Wystarczy jednak odrobina pomysłowości, a nie zaszkodzi również znajomość systemu binarnego oraz podstaw rachunku prawdopodobieństwa. Potrzebujemy rozróżnić na wyjściu 16 różnych stanów (15 dla każdego z modeli i 1 dla gitary, której sieć nie zna). Sprawdźmy, czy zmieścimy się na pięciu wyjściach. Na każdym z wyjść może być 1 lub -1. Oto kilka możliwych kombinacji: (1, 1, -1, -1, -1), (-1, 1, 1, 1, -1), (-1, -1, 1, -1, 1). Każda z nich to wariacja pięcioelementowa z powtórzeniami ze zbioru dwuelementowego (po wyjaśnienia odsyłam do podręczników matematyki dla szkół średnich). Ilość możliwych wariacji k-elementowych ze zbioru n-elementowego opisana jest wzorem:
W naszym przypadku daje to 25, czyli 32. Na pięciu wyjściach zmieścilibyśmy 32 modele gitar! Na 16 modeli potrzebujemy jedynie czterech wyjść (24 = 16).
| Binarnie | Dziesiętnie |
| 0000 | 00 |
| 0001 | 01 |
| 0010 | 02 |
| 0011 | 03 |
| 0100 | 04 |
| 0101 | 05 |
| 0110 | 06 |
| 0111 | 07 |
| 1000 | 08 |
| 1001 | 09 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
A dlaczego mówiłem o systemie binarnym? W tabeli zamieściłem pierwsze 16 liczb dwójkowych i ich wartości dziesiętne (dla przejrzystości podaję liczby binarne na czterech pozycjach, a dziesiętne - na dwóch).
Widać wyraźnie, że na czterech pozycjach, z których każda może przybierać dwie różne wartości (tak, jak wyjście neuronu), można zmieścić 16 różnych informacji. Wszystkie zera zmieniamy w -1 i mamy gotową listę odpowiedzi sieci. Gdy pokażemy jej drugi model gitary, na odpowiednich wyjściach mają się pojawić wartości: (-1, -1, 1, -1). Dla siódmego modelu na wyjściach będzie: (-1, 1, 1, 1). I tak dalej. W ten oto sposób zaoszczędziliśmy na objętości sieci i (co potwierdzają eksperymenty) na czasie uczenia.
Co w środku?
Wiesz już, ilu masz użyć warstw, ilu wejść i ilu wyjść. Pozostaje pytanie o ilość neuronów w warstwach ukrytych.
Warstwami ukrytymi nazywamy wszystkie warstwy sieci oprócz wejściowej i wyjściowej, czyli na przykład dla sieci trzywarstwowej będą to warstwy: pierwsza i druga. Dlaczego "ukryte"? Dlatego, że nie mamy bezpośredniego dostępu do ich wyjść. Sygnały z wyjść warstwy ukrytej trafiają na wejścia następnej warstwy. Użytkownik dostaje dopiero sygnały z wyjść warstwy wyjściowej. Warstwy ukryte pełnią rolę swoistego pośrednika między wejściem a wyjściem. Pozwalają sieci snuć głębsze rozmyślania i dają jej większe możliwości. Z określeniem liczby neuronów warstw ukrytych jest taki problem, że o ile w przypadku warstwy wejściowej i wyjściowej liczba neuronów jest ściśle powiązana z warunkami zadania, to w warstwach ukrytych jest ona praktycznie dowolna. Przeważnie dobiera się ją drogą eksperymentów. Powiedzmy, że mamy sieć dwuwarstwową o dwóch wejściach i jednym wyjściu. Jej strukturę opisuje się tak: 2 - X - 1, gdzie 2 to ilość wejść, X to ilość neuronów w pierwszej warstwie (ukrytej), a 2 - ilość wyjść. Ustalamy X na przykład na 5 i uczymy sieć. Badamy czas uczenia i sprawność nauczonej sieci. Potem zmieniamy wartość X i badamy sieć ponownie. W końcu osiągamy wartość optymalną.
A skoro już wspomniałem o uczeniu sieci - dowiedzmy się w końcu, na czym ono polega.

Start Sieci jednokierunkowe Sieci rekurencyjne Słowniczek Linki O autorach