
Start Sieci jednokierunkowe Sieci rekurencyjne Słowniczek Linki O autorach
Sposób działania sieci neuronowej
Jednym zdaniem...
... jest on dość łatwy do zrozumienia.
Idea działania sieci
Przedstawiłem ową ideę pokrótce w poprzednim rozdziale, jednak pozwolę sobie tutaj ją powtórzyć i nieco rozwinąć. Generalnie sieci używa się na zasadzie: pokażmy jej coś i zobaczmy, jak zareaguje. Czyli w skrócie: pytanie - odpowiedź. Owo pytanie to odpowiednio przetworzone dane (np. obraz, dźwięk, dane giełdowe, warunki pogodowe) przesyłane na wejście sieci. Po "usłyszeniu" pytania sieć podaje odpowiedź - znów są to pewne dane, które projektant sieci potrafi przełożyć na konkretne informacje. Dla tych, którzy uwielbiają schematy blokowe, podaję najprostszy schemat działania sieci:

Będzie najszybciej i najprościej, jeśli dokładniej zasadę działania SSN omówię na przykładzie jej najmniejszego funkcjonalnego fragmentu, jakim jest neuron. Przypominam, że samotny neuron to również "pełnoprawna" sieć.
Jak działa neuron?
Przypominam schemat sztucznego neuronu:
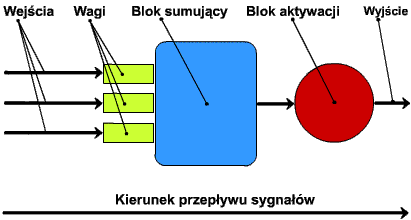
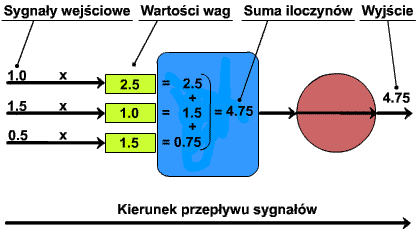
Raz jeszcze zaznaczam, że ilość wejść zależy od specyfiki zadania. Trzy wejścia na tym schemacie to czysty przypadek. Ale wróćmy do zasady działania neuronu: na wejścia trafiają sygnały wejściowe. Są to po prostu liczby opisujące zadanie, które neuron ma rozwiązać. Każda z wag posiada pewną wartość. Sygnały są mnożone przez wartości wag (czyli ważone), wyniki owego mnożenia dodawane są do siebie w bloku sumującym. W ten sposób powstaje konkretna liczba, którą określa się jako potencjał membranowy. Jest ona wysyłana do bloku aktywacji, gdzie może zostać dodatkowo przetworzona. Po ewentualnej operacji wykonanej w bloku aktywacji otrzymujemy gotową odpowiedź neuronu na sygnały wejściowe. Oto przykład z pominięciem bloku aktywacji (za odpowiedź neuronu uznajemy potencjał membranowy):
Teraz parę wyjaśnień a'propos bloku aktywacji. Otóż jest on pewną funkcją, której argumentem jest potencjał membranowy. Innymi słowy: jeśli potencjał membranowy oznaczymy jako j, odpowiedź, czyli wyjście neuronu jako y, a funkcję aktywacji jako f, to operację wykonywaną w bloku aktywacji można zapisać tak:
Odpowiedź neuronu zależy więc od tego, jaką funkcją jest f. W powyższym przykładzie pominęliśmy zupełnie blok aktywacji, jako że przyjąłem, iż funkcja aktywacji będzie funkcją liniową postaci:
... a inaczej:
Zatem wartość owej funkcji, czyli odpowiedź neuronu (f (j)), będzie miała zawsze tę samą wartość, co potencjał membranowy (j). Neuron z taką funkcją aktywacji nazywany jest neuronem liniowym. Za chwilę będziesz mógł przy nim pomanipulować. Najpierw jednak musisz się dowiedzieć, do czego właściwie służą wagi.
Po co wagi?
Funkcjonuje w mowie potocznej określenie: "sprawa dużej wagi". Oznacza to, że jest ona bardzo znacząca dla zainteresowanego. Z neuronem jest podobnie. Wartości pewnych wejść będą dla niego bardziej istotne, niż innych. Każde z wejść ma swoją wagę, czyli informację o tym, jak duże znaczenie dla neuronu ma sygnał podany na to wejście. I tak: wartość wagi mała co do wartości bezwzględnej znaczy, że dane wejście jest niezbyt ważne dla neuronu. Duża wartość dodatnia oznacza, że dane wejście ma duże znaczenie "pozytywne", zaś duża co do wartości bezwzględnej wartość ujemna to znak, iż wejście ma duże znaczenie "negatywne". Wytłumaczę to na przykładzie. Przyjmijmy, że mamy neuron, który "lubi"... samochody. Jako że jest to tylko prosty neuron, to potrafi ocenić jedynie dwie cechy samochodu: czy jest on nowy i czy jest ładny. Taki neuron będzie miał dwa wejścia: jednym z nich wpłynie informacja o wieku auta, zaś drugim - o jego "urodzie". Upodobania neuronu muszą być odzwierciedlone przez wagi tych wejść. Oto kilka przykładowych wartości wag i "charakterystyka" neuronu, którego one dotyczą:
| WAGA "NOWY" | WAGA "ŁADNY" | Co to za neuron? |
| 5 | 1 | Lubi nowe samochody; ich wygląd mało się liczy. |
| 1 | -1 | Wszystko mu jedno... |
| -5 | 4 | Samochód musi być ładny, ale stary. |
| 4 | 5 | Lubi nowe i piękne auta. |
| -4 | -4 | Ekstrawagancki neuron - lubi stare, brzydkie maszyny. |
... i tak dalej, jak mawia Kurt Vonnegut. Proste, nieprawdaż? Teraz zajmijmy się informacjami podawanymi na wejście naszego motoryzacyjnego neuronu. Będą one "mówiły" neuronowi o tym, jaki samochód właśnie przejeżdża obok, zaś neuron wyrazi w odpowiedzi swoją o nim opinię. Jak się zapewne domyślasz, wartości na wejściach będą oznaczały, że samochód jest: brzydki lub stary (-4, -5), taki sobie (-1, 1), lub nowy i ładny (4, 5). Możliwe są oczywiście wartości pośrednie, np. wartość 3 na wejściu odpowiadającym urodzie samochodu oznacza, iż auto jest ładne, ale nie rewelacyjne. Podobnie z wiekiem: jeśli za 5 przyjmiemy samochód najwyżej dwuletni, a za -5 auto z lat dwudziestych, to -2 będzie oznaczało lata pięćdziesiąte.
W tym miejscu muszę odbiec trochę od tematu, by omówić pewną sprawę. Otóż jeśli jesteś informatykiem, to zapewne przyzwyczaiłeś się do tego, że 1 oznacza prawdę, a 0 - fałsz. 1 - TAK, 0 - NIE. Niestety, jeśli chcesz zająć się SSN, musisz się od tego odzwyczaić. W sieciach mianowicie na opisanie dwóch przeciwstawnych stanów używa się raczej liczb przeciwnych. Zatem nie 1 i 0, a 1 i -1. Wynika to z faktu, iż w SSN zero jest sygnałem "pustym", nie niosącym żadnej informacji. Przemnóż zerowy sygnał przez dowolną wagę: wynikiem jest zero. Reasumując: 1 oznacza "tak", -1 - "nie", a 0 - "nieważne". Oczywiście zamiast 1 i -1 można użyć 5 i -5, jak w powyższym przykładzie. Można też wziąć np. 20 i -20. Wszystko zależy od przyjętej skali, a także od rodzaju neuronów (o tym później). Ważne jest, aby skala przyjęta przy ustalaniu wag neuronu odpowiadała mniej więcej skali zastosowanej przy wyznaczaniu sygnałów wejściowych. Tylko wtedy neuron będzie działał poprawnie. Właśnie, a co z odpowiedzią neuronu? Jak będzie się miała do sygnałów wejściowych? Cóż, neuron jest takim mini-mózgiem, więc będzie działał podobnie, jak Ty. Co mówisz, kiedy zobaczysz coś, co Ci się podoba? "Łał, extra, cudo!" A kiedy coś Ci się nie podoba? "Porażka, zabierzcie to". Kiedy coś jest ci obojętne, po prostu wzruszasz ramionami. Neuron zachowuje się podobnie. Nie posiadając Twoich możliwości wyrażania uczuć, zareaguje na swój sposób: duża dodatnia wartość na wyjściu oznacza entuzjazm, duża (co do wartości bezwzględnej) wartość ujemna - dezaprobatę, wartość bliska zeru - obojętność. Jak się zapewne domyślasz, w skali, którą przyjąłem w przykładzie z samochodami odpowiedź neuronu równa 3 znaczyłaby: "całkiem niezły", a -3: "niezbyt mi się podoba".
A jaki samochód będzie się neuronowi najbardziej "podobał"? Znając wartości wag można udzielić odpowiedzi na to pytanie. Jest prosta: dla neuronu ideałem jest taki samochód, którego cechy (wiek i wygląd) są równe wagom odpowiednich wejść neuronu. Kiedy na wejściach pojawią się wartości równe ich wagom, neuron da wysoką odpowiedź. Oczywiście jeśli spotka się z samochodem przewyższającym jego ideał (o wyższych parametrach wieku i wyglądu), wpadnie w jeszcze większy zachwyt (większa wartość na wyjściu).
W tym miejscu dochodzimy do kwestii pamięci neuronu. To, co neuron "wie", zapisane jest w wagach jego wejść. W naszym przypadku jest w nich zapisany wzorzec idealnego samochodu. Podobnie jest w przypadku bardziej skomplikowanej sieci - cała jej wiedza mieści się właśnie w wagach. Nie można przy tym wyodrębnić z owej bazy wiedzy żadnej konkretnej informacji, czy fragmentu sieci odpowiadającego za konkretne zadanie - sieć działa wyłącznie jako całość. Podobnie jest w przypadku ludzkiego mózgu. Wszystko co wiemy, myśli pragnienia, wspomnienia - wszystko jest "zapisane" w połączeniach synaptycznych. Jeśli z jakichś informacji długo nie korzystamy, możemy je zapomnieć - nieużywane połączenia synaptyczne mogą zanikać podobnie, jak nieużywane narządy. W SSN przerwanemu połączeniu odpowiada wejście neuronu z wagą równą 0. Jakikolwiek sygnał, który trafi na wejście, będzie miał po przemnożeniu przez tą wagę zerową wartość i zerowe znaczenie dla wartości wyjścia neuronu.
Ale dość już tej nudnej teorii - zapraszam na poligon doświadczalny.
Dotknij neuronu
Poniżej umieściłem applet będący symulatorem jednego liniowego neuronu. Przyjmijmy, że jest to nasz "motoryzacyjny" neuron. Możesz dowolnie ustawić wartość jego wag i podać dowolne sygnały na jego wejścia. Poobserwuj, jak zmieniają się wartości wyjścia w zależności od ustalonych przez Ciebie parametrów. Szczególnie polecam następujące eksperymenty:
- przy domyślnych wartościach wag ustaw na wejściach wartości równe odpowiednim wagom, przeciwne im, lub bliskie zeru (spróbuj różnych kombinacji);
- ustaw jedną z wag na zero i sprawdź, jak sygnał na tym wejściu wpływa na odpowiedź neuronu;
- porównaj odpowiedzi neuronu z ich objaśnieniami, jakie zamieściłem trzy akapity wyżej;
- spróbuj przewidzieć wartość wyjścia przy ustalonych przez Ciebie wagach i wejściach (algorytm znasz).
Zachęcam do eksperymentowania aż do chwili, w której dokładnie poznasz zasadę działania neuronu i bezbłędnie będziesz przewidywał wartości jego wyjścia. Jeśli będziesz miał kłopoty z appletem, odśwież stronę klawiszem F5 lub przyciskiem na pasku przeglądarki.
Neuron nieliniowy
Małe przypomnienie: neuron oblicza swoje wyjście na podstawie potencjału membranowego, czyli sumy ważonych wejść. Ów potencjał w bloku aktywacji jest przekształcany według pewnej funkcji zwanej funkcją aktywacji neuronu. W neuronie, na którym przed chwilą eksperymentowałeś, funkcja aktywacji była liniowa, a co za tym idzie, wartość na wyjściu neuronu była równa jego potencjałowi membranowemu. Ten neuron był dobry jako model poglądowy, czas jednak zająć się czymś poważniejszym. Aby neuron (sieć neuronowa) był przydatny do większej ilości zadań oraz bardziej odpowiadał działaniu rzeczywistego, biologicznego neuronu, trzeba zastosować w nim nieliniową funkcję aktywacji. Jedna z prostszych funkcji stosowanych w tym przypadku (szerzej omówię to zagadnienie w części "dla fachowców") to tak zwana bipolarna funkcja skoku jednostkowego. Nie przerażaj się nazwą, tak naprawdę jest to bardzo prosta funkcja. Oto jej wykres:
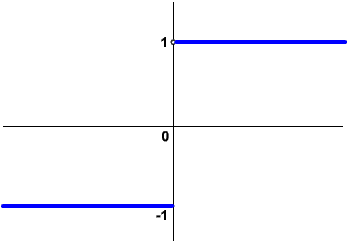
Jak widać na wykresie, dla wartości potencjału membranowego mniejszych lub równych zeru wyjście neuronu przyjmie wartość -1, zaś dla większych od zera - wartość 1. Oznacza to, że tam, gdzie nasz liniowy motoryzacyjny wektor "mówił": 2, 3, 4.5 - wektor nieliniowy powie krótko: 1. Nie będzie dawał tak subtelnych i ostrożnych odpowiedzi, lecz kategoryczne: 1 lub -1. Tak lub nie, wszystko albo nic. Prawdę mówiąc bliższa biologicznemu neuronowi byłaby funkcja unipolarna, czyli taka, w której zamiast -1 zastosowano 0:
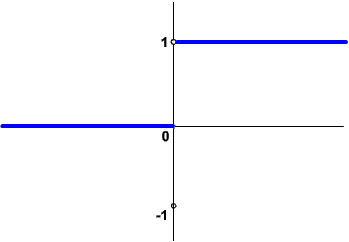
W SSN jednakże raczej unika się sygnałów o wartości 0, stąd funkcja bipolarna.
Poniżej znajduje się applet symulujący neuron nieliniowy. Możesz wykonywać na nim te same operacje, co na neuronie liniowym z pierwszego appletu - zmiana wag i wejść. Postaraj się uchwycić moment zmiany wartości wyjścia w zależności od wejść. Zauważ, jak niewielka modyfikacja wystarczy, aby całkowicie zmienił się stosunek neuronu do zadanego obiektu (który jest opisany przez wartości wejść). Poznęcaj się nad tym neuronem, nie żałuj sobie. Do dzieła!
Taki neuron jest możemy nazwać perceptronem, a dokładniej - perceptronem prostym. Na jego wyjściu pojawiają się tylko dwa rodzaje sygnałów: 1 (akceptacja) i -1 (odrzucenie). Służy on zazwyczaj do rozpoznawania pewnych obiektów.
A w sieci?
Kolejny applet pozwoli ci popracować z jednowarstwową nieliniową najprawdziwszą siecią neuronową. Będzie ona wprawdzie miała tylko trzy neurony, ale to nam na razie wystarczy. Jest jedna duża różnica między tym appletem a poprzednimi. Wcześniej miałeś dostęp do wartości wag i mogłeś je bezpośrednio zmieniać. Teraz do ich ustalenia wykorzystamy proces uczenia. Nie będziemy się póki co wgłębiać w szczegóły - o tym w następnym rozdziale. Nasza przykładowa sieć wygląda tak:
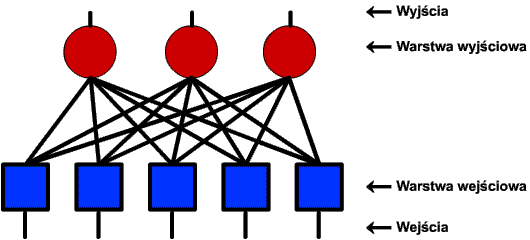
Jak widzisz, mamy tu pięć wejść. Sieć owa rozpoznaje obiekty, które mają pięć cech charakterystycznych (po jednej na każde wejście). Przykładowy obiekt podawany na wejście może wyglądać tak: 3, 4, -1, 2, 3. Albo: -3, 4, -3, 1, -2. I tak dalej. Wiesz już, że perceptron działa na zasadzie klasyfikacji: akceptacja / odrzucenie. Skoro mamy trzy neurony, to możemy każdy z nich nauczyć rozpoznawania pewnego obiektu. Co więcej, obiekt ten dwa pozostałe neurony powinny odrzucać. Trzeba zatem określić trzy rozpoznawane obiekty i każdemu z nich przyporządkować żądane wyjście sieci. Na przykład: dla obiektu: 1, 3, -2, 4, 4; na wyjściu ma być: 1, -1, -1. Oznacza to, iż ten obiekt jest rozpoznawany (i akceptowany) przez pierwszy neuron (dwa pozostałe reagują negatywnie). Jeśli dla obiektu: 4, -2, -2, 1, -3; ustawimy wyjście: -1, 1, -1; to obiekt ten będzie rozpoznawany przez drugi neuron. Na tym mniej więcej polega uczenie sieci: pokazuje się jej wzorcowy obiekt, który powinna rozpoznawać oraz wartość, która powinna się pojawić na jej wyjściu po podaniu na wejście tego obiektu. Po ludzku: pokazujemy sieci obiekt i podpowiadamy jej, jak ma na niego reagować. Zgodnie z pewnym algorytmem sieć zmienia swoje współczynniki wag, aby dopasować swe działanie do żądanego przez nauczyciela.
Jeszcze kilka wyjaśnień co do obsługi appletu. Trzy pięcioczęściowe okienka na dole zawierają trzy obiekty, które sieć powinna rozpoznawać. Pierwszy z nich ma być rozpoznawany przez pierwszy neuron (czyli odpowiedź sieci wynosi: 1, -1, -1), drugi - przez drugi neuron (-1, 1, -1), a trzeci - sam się domyśl. J Kiedy wprowadzisz obiekty wzorcowe (lub skorzystasz z domyślnych), naciśnij przycisk z etykietą "Uczenie". Dopóki sieć się uczy (trwa to ułamek sekundy), przycisk "Rozpoznawanie" jest - na wszelki wypadek - nieaktywny. Po zakończeniu uczenia możesz wprowadzić do okienka na środku ekranu liczby oznaczające obiekt do rozpoznania i za pomocą przycisku "Rozpoznawanie" sprawdzić reakcję sieci na ten obiekt.
Zapraszam do eksperymentów. Polecam:
- podać na wejście obiekt podobny do rozpoznawanego przez któryś z neuronów;
- nauczyć dwa neurony rozpoznawania podobnego obiektu;
- zwrócić uwagę na obiekt, który jednocześnie jest rozpoznawany przez dwa lub trzy neurony;
- spróbować nauczyć sieć rozpoznawania następujących obiektów: pierwszy złożony tylko z jedynek (1, 1, 1, 1, 1), drugi - z dwójek, a trzeci - z trójek.
Z powyższego przykładu wynika bardzo ważny wniosek: sieć nie uczy się podanych obiektów "na pamięć", ale wychwytuje pewne ich charakterystyczne cechy. Dowodzi tego fakt, iż zdolna jest rozpoznać obiekt podobny do zadanego. Ta cecha sieci nazywa się zdolnością do uogólniania zdobytej wiedzy. Zauważ, że sieć zachowuje się często jak dziecko, które zobaczywszy konia woła: "muu!", bo wcześniej rodzice pokazali mu krowę. Mózg dziecka uogólnił wiedzę: jeśli coś ma cztery nogi i je trawę, to jest to "mu". W tym przypadku oczywiście wniosek dziecka jest błędny, tym nie mniej sama zdolność uogólniania wiedzy jest bardzo przydatna.
Teraz możesz przeprowadzić jeszcze jeden ciekawy eksperyment z tym appletem. Jeśli po nauczeniu sieci pewnych wzorców ponownie naciśniesz przycisk "Uczenie", sieć zostanie "douczona" podanych wzorców. Możesz to zauważyć w następujący sposób: po jednorazowym nauczeniu sieci pewnych wzorców podaj na wejście obiekt "podobny" do dwóch różnych wzorców wejściowych jednocześnie. Postaraj się podać taki obiekt, który zaakceptują dwa neurony. Następnie kilka razy doucz sieć i powtórz próbę rozpoznania tego obiektu. Jeśli sieć douczyła się porządnie, to najprawdopodobniej (bo z SSN to nigdy nic nie wiadomo) teraz obiekt zostanie rozpoznany przez tylko jeden neuron. Drugi neuron "zrozumie", że się mylił - podany obiekt nie jest aż tak podobny do jego wzorca. Odpowiada to z grubsza sytuacji, kiedy dziecko nie traktuje już jako konia jako krowy, bo widzi, że krowa powinna mieć rogi.
Jeśli próbowałeś bezskutecznie nauczyć sieć rozpoznawania obiektu, o którym pisałem w ostatnim z poleceń powyżej appletu, zapewne dziwisz się, dlaczego tak się zachwycam sieciami neuronowymi, skoro ta tutaj "wyłożyła się" na tak prostym zadaniu. Wszystko jednak jest w porządku i zostanie wyjaśnione w następnym rozdziale.
Sieć, którą się zajmowaliśmy, składała się z jednej warstwy (nie licząc warstwy wejściowej). Na następnej stronie wyjaśnię, kiedy i dlaczego warto użyć większej ilości warstw, czyli omówię problem wyboru struktury SSN.

Start Sieci jednokierunkowe Sieci rekurencyjne Słowniczek Linki O autorach