Adaline i Madaline

Adaline

W literaturze można spotkać dwie definicje struktury Adaline. Pierwsza określa ją jako liniowy element przetwarzający, którego sygnał wyjściowy opisany jest następująco:

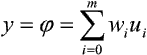
przy czym indeks i = 0 dotyczy elementu progowego z doprowadzonym sygnałem u₀ zawsze równym 1. Wprowadzenie ewentualnego stałego współczynnika liniowego k jest jedynie zmianą ilościową, a nie jakościową. W przypadku włączenia elementu Adaline w strukturę sieci wielowarstwowej rolę tego współczynnika przejmują wagi połączeń wychodzących z elementu.

Inna definicja niczym nie wyróżnia struktury Adaline od elementu perceptronowego. Obok sumatora (zwanego także ALC, czyli z ang. Adaptive Linear Combiner) istnieje blok aktywacji realizujący bipolarną funkcję signum:

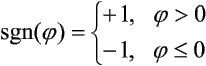
Istnieje jednak istotna różnica pomiędzy elementem perceptronowym a elementem typu Adaline, niezależnie od definicji jego struktury. Jest nią reguła uczenia Adaline, która opiera się na metodzie minimalizacji błędu średniokwadratowego, znanej dla układów liniowych. Przy podejmowaniu decyzji o ewentualnej zmianie wag w perceptronie uwzględnia się wartość wyjściową z bloku aktywacji, w przypadku Adaline natomiast wykorzystuje się wynik sumatora ALC. Oto schemat procesu uczenia Adaline:

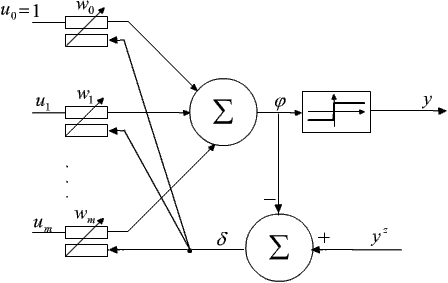
Załóżmy, że mamy pewien L-elementowy zbiór:

składający się z par wektorów wejściowych u^m i odpowiadających im zadanych wartości wyjściowych y_m^z (m = 1, 2, ..., L). Będziemy poszukiwać takiego algorytmu, aby w procesie kolejnych prezentacji danych wejściowych u uzyskiwać coraz korzystniejsze wartości wektora w w sensie najlepszego przybliżenia obrazu wyjściowego sieci y do obrazu zadanego y^z. Do wektora wag wprowadzamy kolejne poprawki po każdej prezentacji (u^m, y_m^z) Î G tak długo, aż na wyjściu bloku ALC będą otrzymywane poprawne odpowiedzi.

Miarą poprawności wektora wag w jest różnica pomiędzy oczekiwaną a otrzymaną wartością wyjściową:

Algorytm powinien minimalizować wartość oczekiwaną kwadratu błędu (błąd średniokwadratowy) dla pewnego rozkładu prawdopodobieństwa kolejnych prezentacji, tzn. określić minimum wyrażenia:

po wszystkich punktach przestrzeni wag.

Korzystając z poprzedniego równania otrzymamy:

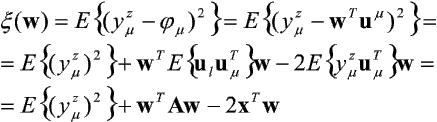
gdzie A = Eíu_lu_m^Tý jest wejściową macierzą korelacji; x = Eíy_m^zu^mý. Przy takim sformułowaniu problemu wyznaczania najlepszych wartości elementów wektora wag w^* sprowadza się do zagadnienia minimalizacji błędu średniokwadratowego przy założonej strukturze sieci i przyjętym modelu neuronu. Warunkiem koniecznym osiągnięcia minimum przez wskaźnik x jest zerowanie się gradientu:

Stąd otrzymamy:

Jak łatwo zauważyć, analityczne wyznaczenia wektora wag w^* na podstawie powyższego wzoru jest w ogólnym przypadku dość trudne, gdyż do właściwego wyznaczenia macierzy A i wektor x wymagana jest znajomość odpowiednich rozkładów prawdopodobieństwa.

Wygodniejsze jest zastosowanie metody iteracyjnej, która zakłada wprowadzenie poprawek do wartości elementów wektora wag w procesie kolejnych prezentacji elementów zbioru G. Niech k numeruje kolejne iteracje. Wówczas, przyjmując pewien początkowy wektor wag w(0), procedura taka przyjmuje postać:

gdzie Dw(k) jest poprawką wektora wag w k-tej iteracji. Kierunek wektora Dw(k) powinien zapewnić możliwie najszybsze zbliżanie się do optymalnego wektora wag w^*, czyli być kierunkiem najszybszego spadku funkcji x w punkcie w(k) przestrzeni wag. Wynika stąd, że powinien on być antyrównoległy do gradientu tej funkcji, czyli:

gdzie h jest pewną stałą dodatnią.

Wyznaczenie wartości owego gradientu wymaga jednak znajomości macierzy A oraz wektora x. Można przybliżyć x kwadratem błędu wyznaczonego na k-tej iteracji dla m-tego elementu G:

Po zróżniczkowaniu otrzymujemy:

Stąd uaktualniony wektor wag wyraża się wzorem:

Ostatecznie algorytm uczenia przyjmuje postać:

1. Wprowadź na wejście elementu Adaline wektor wejściowy u^m.
2. Wyznacz błąd x_m(k) według wzoru:
   
   
   
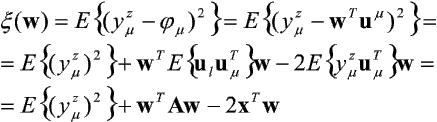
3. Wyznacz nowy wektor wag w(k + 1) według wzoru:
   
   
   
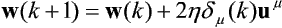
4. Powtarzaj kroki 1 - 3 tak długo, aż suma kwadratów błędów dla zbioru G nie stanie się wystarczająco mała, tzn. mniejsza od zadanej dokładności.

Wzór, według którego wyznacza się nowy wektor wag, określa tzw. regułę uczenia Widrowa - Hoffa, opartą na metodzie najmniejszego błędu średniokwadratowego, stąd współistniejąca nazwa - reguła LMS (ang. Least-Mean-Square). W literaturze używana jest też nazwa: reguła delty.

Madaline

Jak łatwo zauważyć, budowa i zasada działania Adaline jest zbliżona do pojedynczego elementu perceptronowego i podlega podobnym ograniczeniom, np. przy pomocy Adaline z dwoma wejściami nie można rozwiązać problemu XOR. Podobnie jak przy budowaniu sieci wielowarstwowych z elementów perceptronowych, z elementów Adaline można utworzyć sieć, która nazywa się siecią typu Madaline. Struktura ogólna takiej sieci może być identyczna ze strukturą perceptronu wielowarstwowego.

W zasadzie złożona struktura sieci Madaline komplikuje poszukiwanie efektywnej metody jej uczenia. Zachęcająca jest idea użycia algorytmu LMS. Metoda ta jednak wymaga znajomości wejść i zadanych wyjść dla każdej z warstw, w tym warstw ukrytych, dla których informacji takiej nie posiadamy. Ponadto algorytm LMS dotyczy wyjść sumatora ALC, a nie bipolarnych wartości wyjściowych Adaline. Należy zatem określić inną strategię uczenia dla bloku aktywacji.

Możliwe jest zastosowanie do uczenia struktur podobnych do Madaline metody bazującej na algorytmie LMS, chociaż wymaga to wprowadzenia w miejsce funkcji progowej funkcji różniczkowalnej. Taka metoda to algorytm propagacji wstecznej, o którym będzie mowa w następnym rozdziale.

Rozważmy tymczasem metodę zwaną MRII, czyli Madaline rule II. Przypomina ona metodę prób i błędów, z dodatkiem odrobiny "inteligencji" w postaci zasady minimalnego zaburzenia. Idea metody MRII zawiera się w poniższym algorytmie:

1. Podaj wektor uczący na wejście Madaline i wyznacz odpowiedź warstwy wyjściowej.
2. Oblicz liczbę niepoprawnych wartości w warstwie wyjściowej. Liczba ta będzie miarą dokładności (błędem).
3. Dla wszystkich elementów warstwy wyjściowej:
   • wybierz pierwszy (wcześniej nie wybrany) element, dla którego wynik ważonego sumowania w bloku ALC jest najbliższy zeru (w takim elemencie niewielka zmiana wag spowoduje odwrócenie znaku na bipolarnym wyjściu bloku aktywacji, stąd określenie "zasada minimalnego zaburzenia");
   • zmień wagi wybranego elementu tak, aby zmienić wartość jego wyjścia z bloku aktywacji;
   • ponownie wyznacz wektor wyjściowy dla wejściowego wektora uczącego;
   • jeśli w wyniku zmiany wag zmniejszył się błąd (tzn. ilość wyjść bipolarnych różnych od wzorcowych), zaakceptuj te zmiany, w przeciwnym razie powróć do wag poprzednich.
4. Powtórz krok 3 dla wszystkich pozostałych warstw za wyjątkiem warstwy wejściowej.
5. Dla wszystkich elementów warstwy wyjściowej:
   • wybierz (wcześniej nie wybraną) parę elementów, dla których ważona suma wejść w bloku ALC jest bliska zeru;
   • zmień wago wybranych elementów tak, aby zmienić wartość ich wyjść z bloku aktywacji;
   • ponownie wyznacz wektor wyjściowy dla wejściowego wektora uczącego;
   • jeśli w wyniku zmiany wag zmniejszył się błąd, zaakceptuj te zmiany, w przeciwnym razie powróć do stanu poprzedniego.
6. Powtórz krok 5 dla wszystkich pozostałych warstw za wyjątkiem warstwy wejściowej.

Jeśli zajdzie konieczność, krok 5 i 6 może być powtarzany dla układów trypletowych, kwadrupletowych i większych kombinacji elementów.