Algorytm wstecznej propagacji błędów

Jest to podstawowy algorytm uczenia nadzorowanego wielowarstwowych jednokierunkowych sieci neuronowych. Podaje on przepis na zmianę wag w_ij dowolnych połączeń elementów przetwarzających rozmieszczonych w sąsiednich warstwach sieci. Oparty jest on na minimalizacji sumy kwadratów błędów uczenia z wykorzystaniem optymalizacyjnej metody największego spadku. Dzięki zastosowaniu specyficznego sposobu propagowania błędów uczenia sieci powstałych na jej wyjściu, tj. przesyłania ich od warstwy wyjściowej do wejściowej, algorytm propagacji wstecznej stał się jednym z najskuteczniejszych algorytmów uczenia sieci.

Reguła delty i metoda największego spadku

Rozważmy sieć jednowarstwową o liniowych elementach przetwarzających. Załóżmy, że mamy P-elementowy zbiór wzorców. Przy prezentacji m-tego wzorca na wejściu sieci, dla j-tego elementu wyjściowego możemy zdefiniować błąd:

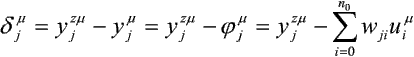
gdzie y_j^zm, y_j^m i j_j^m oznaczają odpowiednio oczekiwane i aktualne wartości wyjścia j-tego elementu oraz ważoną sumę wejść wyznaczoną w jego sumatorze przy prezentacji m-tego wzorca; u_i^m - ita składowa m-tego wektora wejściowego (u₀^m = 1, wejście progowe); w_ij oznacza wagę połączenia pomiędzy j-tym elementem warstwy wyjściowej a i-tym elementem warstwy wejściowej; n₀ - liczba wejść.

Jako miarę błędu sieci x wprowadźmy sumę po wszystkich wzorcach błędów powstałych przy prezentacji każdego z nich:

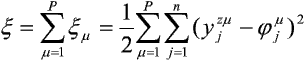
gdzie:

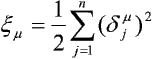
przy czym n oznacza liczbę elementów w warstwie wyjściowej.

Problem uczenia sieci to zagadnienie minimalizacji funkcji błędu x. Jedną z najprostszych metod minimalizacji jest gradientowa metoda największego spadku. Jest to metoda iteracyjna, która poszukuje lepszego punktu w kierunku przeciwnym do gradientu funkcji celu w danym punkcie. Stosując powyższą metodę do uczenia sieci, zmiana Dw_ji wagi połączenia w_ji winna spełniać relację:

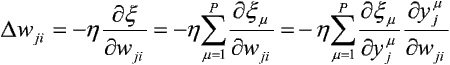
gdzie h oznacza współczynnik proporcjonalności.

W przypadku liniowych elementów przetwarzających mamy:

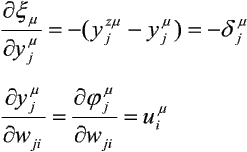
Stąd otrzymamy:

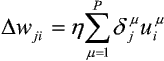
Ostatecznie pełną regułę wyznaczania wag połączeń zapiszemy:

gdzie górne indeksy n i s oznaczają odpowiednio "nową" i "starą" wartość współczynnika wag w_ji.

Konsekwentna realizacja metody największego spadku wymaga dokonywania zmian wag w_ji dopiero po zaprezentowaniu sieci pełnego zbioru wzorców, m = 1, 2, ..., P. W praktyce stosuje się jednak zmiany wag po każdej prezentacji pojedynczego wzorca zgodnie ze wzorem:

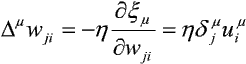
co pozwala istotnie uprościć praktyczną realizację algorytmu.

Zasada zmiany wartości współczynników wag w_ji, określona powyższym wzorem, nazywana jest regułą delty. Owa modyfikacja wprowadza wprawdzie pewne zaburzenie do metody największego spadku, ale jest ono zaniedbywalnie małe dla odpowiednio niewielkich wartości h, czyli dla małych zmian wag. Reguła delty, jako pewne przybliżenie metody największego spadku przy wystarczająco małym współczynniku h, poszukuje zbioru wag minimalizującego funkcję błędu sieci liniowej.

Uogólniona reguła delty

Rozważmy sieć jednowarstwową z elementami przetwarzającymi o nieliniowej, lecz niemalejącej i różniczkowalnej funkcji aktywacji f. Wówczas zmianę wag w_ji można opisać równaniem:

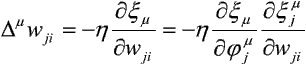
Druga z pochodnych cząstkowych jest oczywiście równa u_i^m. Pierwsza dla elementu liniowego jest równa -d_j^m. Przez analogię zdefiniujemy nową zmienną:

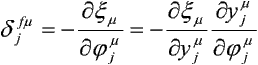
przy czym:

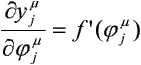
gdzie f'(j) oznacza pochodną funkcji aktywacji względem zmiennej j.

Stąd na podstawie zamieszczonych wyżej wzorów zapiszemy:

Ostatecznie wzór ogólny przyjmie postać:

i nosi nazwę uogólnionej reguły delty dla nieliniowej sieci jednowarstwowej.

Rozważmy M-warstwową sieć elementów o jednakowych nierosnących i różniczkowalnych funkcjach aktywacji f(j):

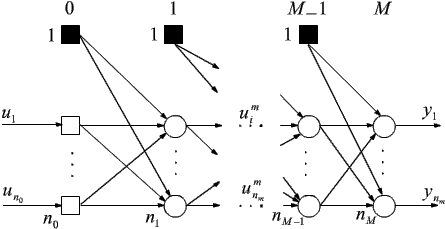
Jeśli przez u_i^mm oznaczymy wartość wyjścia i-tego elementu m-tej warstwy przy prezentacji m-tego wzorca (m = 0, ..., M; i = 0, 1, ..., n_m; m = 1, 2, ..., P), to aktywność j-tego elementu przetwarzającego m-tej warstwy wyrazi się wzorem:

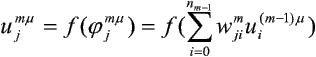
Zdefiniujmy błąd powstały w j-tym elemencie m-tej warstwy, analogicznie do wzoru:

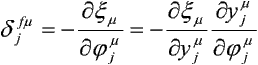
czyli:

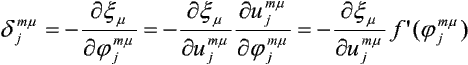
Dla warstwy wyjściowej zgodnie z wzorem:

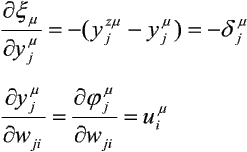
zapiszemy:

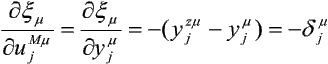
Powyższa pochodna cząstkowa jest bardziej kłopotliwa do wyznaczenia dla elementów warstw ukrytych, ze względu na złożoność zależności x^m od u_j^mm. Należy pamiętać, że u_j^mm jest jednym za składników sum ważonych liczonych we wszystkich elementach warstwy (m + 1). Możemy zatem napisać:

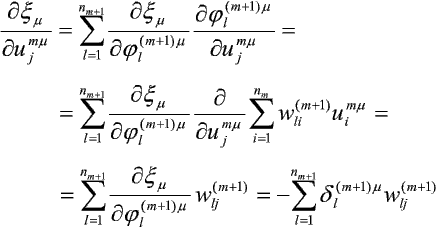
Stąd, na podstawie trzech ostatnich zależności, możemy każdemu elementowi przetwarzającemu przypisać błąd:

• dla warstwy wyjściowej:
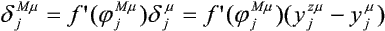
• dla warstw ukrytych:

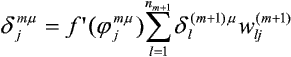
Dla tak zdefiniowanego błędu możemy wyprowadzić ogólną regułę delty:

Uogólniona reguła delty jest procedurą dwufazową. W pierwszej fazie na wejściu sieci prezentowany jest wektor wzorcowy u^m i dla każdej warstwy wyznacza się aktualne aktywności wszystkich elementów przetwarzających zgodnie ze wzorem:

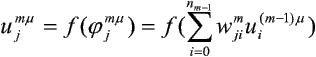
Fazę tą kończy porównanie aktywności elementów wyjściowych y_j^m, j = 1, 2, ..., n_M z oczekiwanymi wyjściami y_j^zm. W drugiej fazie błąd warstwy wyjściowej d_j^Mm jest rzutowany wstecz zgodnie ze wzorem:

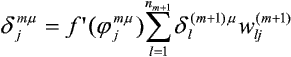
na wszystkie elementy przetwarzające sieci w kolejności przeciwnej do uporządkowania warstw:

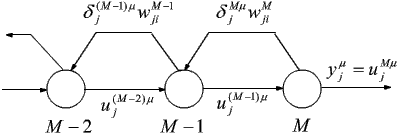
Po określeniu wartości błędów dla każdego elementu przetwarzającego warstw ukrytych pozostaje jedynie wyznaczenie poprawek wag połączeń przy pomocy wzoru:

Technika polegająca na przesyłaniu błędów warstwy wyjściowej wstecz poprzez sieć w celu określenia odpowiednich zmian wag w warstwach wcześniejszych nazwana została wsteczną propagacją błędów, i stąd nazwa metody uczenia.

Osobliwości algorytmu

Ogólnie algorytm propagacji wstecznej wymaga dla każdego wzorca uczącego wykonania następujących działań:

1. Podaj wektor uczący u^m na wejście sieci.
2. Wyznacz wartości wyjść u_j^mm każdego elementu dla kolejnych warstw przetwarzania neuronowego, od pierwszej warstwy ukrytej do warstwy wyjściowej.
3. Oblicz wartości błędów d_j^Mm dla warstwy wyjściowej.
4. Oblicz wartość sumy kwadratów błędów x_m.
5. Dokonaj propagacji wstecznej błędu wyjściowego d_j^Mm do poszczególnych elementów warstw ukrytych wyznaczając d_j^mm według wzoru:
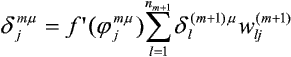
6. Dokonaj aktualizacji wag kolejno pomiędzy warstwą wyjściową i ukrytą, a następnie pomiędzy warstwami ukrytymi przesuwając się w kierunku warstwy wejściowej.

Zauważmy, że wartości błędów elementów danej warstwy ukrytej wyznaczane są przed aktualizacją wag w warstwie następnej, co ma istotne znaczenie dla poprawności algorytmu, choć niekiedy rezygnuje się z tego ograniczenia. Kolejność aktualizacji wag w danej warstwie nie jest istotna. Wyznaczona wartość błędu x_m wykorzystywana jest do określenia jakości stanu sieci na danym etapie uczenia. Jeśli owa wartość jest mniejsza od zadanej dokładności dla wszystkich m = 1, 2, ..., P, tzn. dla wszystkich wzorców uczących, to proces uczenia może być zakończony.

W trakcie procesu uczenia sieci można wykorzystać dowolną liczbę wzorców uczących. W praktyce do uczenia używa się zazwyczaj stosunkowo niewielu wzorców, a przy pomocy pozostałych sprawdza się, czy nauczona sieć realizuje prawidłowe odwzorowanie. Zbiór wzorców dzielony jest więc faktycznie na dwa zbiory: uczący oraz testujący.

Jeśli sieć będzie pracowała z danymi zakłóconymi, to część wektorów uczących powinna być również "wzbogacona" o zakłócenia. Wiąże się to ze zdolnością sieci do uogólniania. Często niewielkie zaburzenie sygnałów wzorcowych powoduje przyspieszenie zbieżności procesu uczenia, pomimo że w rzeczywistym układzie pracy zaburzony sygnał nigdy się nie pojawi.

Zdolność sieci typu propagacji wstecznej do uogólnień polega na tym, że przy danym zbiorze uczącym sieć znajduje pewne wspólne cechy wektorów uczących. Podanie wektora wejściowego, który nie był prezentowany w czasie uczenia, powoduje zakwalifikowanie go do jednej z określonych klas wektorów, a wyjście sieci powinno być zbliżone do wyjścia odpowiadającego najbliższemu wzorcowi w przestrzeni wejść. Sieć typu propagacji wstecznej nie dokonuje jednak ekstrapolacji. Nie można właściwie przyporządkować danego wektora wejściowego, jeśli klasa, do której należy, nie miał swojej reprezentacji w zbiorze wektorów uczących. Należy zatem poprzez odpowiedni dobór wektorów uczących zapewnić w miarę możliwości pokrycie całej przestrzeni stanów wejściowych. Istotna jest też kolejność prezentacji wzorców uczących. Należy unikać sytuacji, kiedy prezentowane są wzorce najpierw jednej klasy, potem drugiej, itd., ponieważ sieć "zapomina" wzorce wcześniej zapamiętane. Najskuteczniejsza jest losowa kolejność prezentacji wzorców, podobnie jak w przypadku perceptronu prostego.

Pierwszą operacją w procesie uczenia sieci jest inicjalizacja początkowego układu wag połączeń między elementami sieci. Należy unikać symetrii w warstwach wag początkowych. Jeśli wagi na początku przyjmują identyczne wartości, a rozwiązanie zagadnienia wymaga istnienia wag o różnych wartościach, to sieć może nigdy się nie nauczyć. Spowodowane jest to faktem, że rzutowany wstecz błąd warstwy wyjściowej jest proporcjonalny do wag połączeń. Jeśli wagi są sobie równe, to poprawki do wag w danej warstwie też są sobie równe i zróżnicowanie wag nigdy nie nastąpi. Odpowiednikiem tej sytuacji w metodzie największego spadku jest start z punktu będącego lokalnym maksimum lub punktem siodłowym funkcji celu, gdzie gradient jest równy zeru i nie można wskazać kierunku poszukiwań minimum. Najskuteczniejszym rozwiązaniem jest losowy dobór wag, co praktycznie całkowicie zabezpiecza przed problemem z symetrią. Reguła ta obowiązuje również dla połączeń z wejściem progowym.

Istotną rzeczą jest umiejętny dobór współczynnika uczenia h. Parametr ten ma ogromny wpływ na stabilność i szybkość całego procesu. Przy zbyt małej wartości współczynnika uczenie sieci jest bardzo wolne. W przypadku dużej jego wartości algorytm może stać się niestabilny i nie być w stanie osiągnąć optymalnego punktu w przestrzeniu wag. Wartość h dobiera się zazwyczaj z przedziału [0.05; 0.25].

Przyspieszenie zbieżności algorytmu, przy jednoczesnym zachowaniu stabilności, możliwe jest przy zastosowaniu techniki momentum. Zgodnie z tą techniką zmiana wag dla (k + 1)-ej prezentacji wzorca wyraża się wzorem:

gdzie h, podobnie jak wyżej, jest parametrem uczenia; a jest stałą dodatnią określającą wpływ poprzedniej zmiany wag na zmianę dokonywaną aktualnie. Drugi człon prawej strony równania, zwany członem momentum, nadaje całemu wyrażeniu własność filtru dolnoprzepustowego, co eliminuje gwałtowne zmiany wartości funkcji błędu x w przestrzeni wag. Zwykle proponuje się przyjęcie dla a wartości nieco poniżej 1 (np. a = 0.9). Pozwala to na zwiększenie współczynnika h do wartości z przedziału [0.25; 0.75].

Niestety, algorytm propagacji wstecznej nie gwarantuje znalezienia globalnego minimum funkcji x w przestrzeni wag, gdy funkcja ta charakteryzuje się bogatą topologią. Proces uczenia przy pomocy algorytmu propagacji wstecznej opiera się na metodzie największego spadku, która nie posiada zdolności wyznaczania minimum globalnego. W przypadku, kiedy osiągamy optimum lokalne, i wszystkie błędy x_m dla każdego wzorca mają wartość poniżej zadanej dokładności, z punktu widzenia "nauczyciela" takie rozwiązanie jest satysfakcjonujące. Jednakże dla pewności otrzymanego rozwiązania proces uczenia należy powtórzyć po wprowadzeniu pewnych modyfikacji do struktury sieci lub algorytmu w zakresie:

• zmiany liczby elementów w warstwach ukrytych;
• zmiany wartości współczynników uczenia i momentum;
• zmiany wartości wag początkowych (np. zmiana zakresu, z którego są losowane początkowe wartości) w taki sposób, aby stan początkowy sieci znalazł się na obszarze innej "doliny" funkcji x w przestrzeni wag.

Wybór odpowiedniej techniki zależy od "nauczyciela".

Naciśnij strzałkę aby wrócić do spisu treści.