Perceptron

Historia

W roku 1958 Rosenblatt opracował i zbudował sztuczną sieć neuronową nazwaną perceptronem. Ten częściowo elektromechaniczny, a częściowo elektroniczny układ przeznaczony był do rozpoznawania znaków alfanumerycznych z procesem uczenia jako metodą programowania systemu. Ważnym rezultatem Rosenblatta było ponadto udowodnienie tzw. twierdzenia o zbieżności perceptronu, które gwarantuje skończoną liczbę iteracji procesu uczenia, o ile dla zagadnienia modelowanego przy użyciu tego typu sieci optymalny układ wag istnieje. Pomimo iż działanie perceptronu nie było zadowalające z punktu widzenia zasadniczego celu (układ wykazywał dużą wrażliwość na zmianę skali rozpoznawanych obiektów oraz ich położenia w polu widzenia), był to ogromny sukces badań prowadzonych w tym zakresie. Przede wszystkim był to pierwszy fizycznie skonstruowany układ symulujący sieć nerwową, który wraz ze zdolnością do uczenia się wykazywał zdolność do poprawnego działania nawet po uszkodzeniu części jego elementów. W swojej najprostszej postaci perceptron zbudowany był z dwóch oddzielnych warstw neuronów reprezentujących odpowiednio wejście i wyjście:

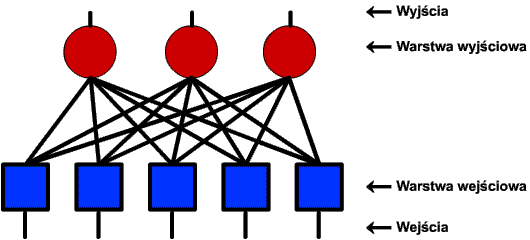
Zgodnie z przyjętą zasadą neurony warstwy wyjściowej otrzymują sygnały od neuronów warstwy wejściowej, lecz nie odwrotnie. Oprócz tego neurony z danej warstwy nie komunikują się między sobą.

Perceptron prosty

Idea perceptronu jest zawarta w następujących zasadach:

1. Elementem składowym perceptronu jest sztuczny neuron, którego model matematyczny może być opisany funkcją aktywacji unipolarną:
   
   
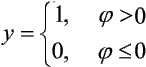
   lub bipolarną:
   
   
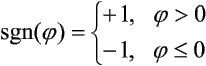
   gdzie:
   
   
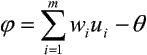
   przy czym w_i oznacza wagę i-tego połączenia wstępującego do elementu; u_i - wartość i-tego wejścia; q - wartość progową funkcji aktywacji.
2. Sieć perceptronową można podzielić jednoznacznie na ściśle uporządkowane i rozłączne klasy elementów zwane warstwami, wśród których wyróżnić można warstwę wejściową i wyjściową. Pozostałe noszą nazwę warstw ukrytych.
3. Perceptron nie zawiera połączeń pomiędzy elementami należącymi do tej samej warstwy.
4. Połączenia pomiędzy warstwami są asymetryczne i skierowane zgodnie z ich uporządkowaniem, tzn. od warstwy wejściowej do pierwszej warstwy ukrytej, następnie od pierwszej do drugiej warstwy ukrytej, itd. aż do warstwy wyjściowej. Nie ma połączeń zwrotnych.

Warstwa wejściowa posiada elementy o nieco uproszczonej funkcji przejścia i jednym wejściu. Jest to swego rodzaju układ receptorów odbierających sygnały wejściowe i po wstępnym ich przetworzeniu (np. normalizacji, filtracji) przesyłających je do elementów warstwy następnej. Umownie jest to warstwa zerowa sieci. Stąd perceptron zawierający jedynie warstwę wejściową i wyjściową nazywany jest perceptronem jednowarstwowym lub perceptronem prostym.

W praktycznych zastosowaniach SSN (sztucznym sieci neuronowych) ustala się dla każdego elementu przetwarzającego wartość progu q = 0. Jego rolę przejmuje waga wstępującego do niego połączenia od dodatkowego elementu wejściowego (tzw. elementu progowego, ang. bias) o wartości u₀ zawsze równej 1. Wówczas dla w₀ = - q wzór:

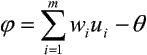
przyjmuje postać:

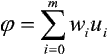
Zaletą powyższej modyfikacji jest uzyskania jednolitych wzorów określających zmiany wag i progów aktywacji w procesie uczenia sieci (dostrajania parametrów sieci).

Najprostszą siecią jednokierunkową jest perceptron prosty. Zbudowany jest jedynie z warstwy wejściowej i wyjściowej. Ponieważ nie istnieją połączenia między elementami warstwy wyjściowej, każdy z nich można potraktować niezależnie jako osobna sieć o m+1 wejściach i jednym wyjściu.

Rozpatrzmy proces uczenia nadzorowanego dla tego typu elementu sieci.

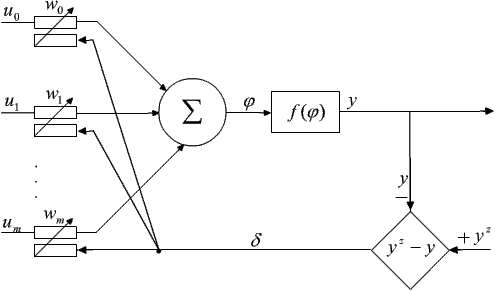
Przyjmijmy, że w bloku aktywacji elementu przetwarzającego realizowana będzie funkcja unipolarna:

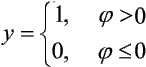
Dany jest pewien zbiór wzorcowych wektorów wejściowych u Î R^m+1 i odpowiadających im oczekiwanych wartości wyjściowych y^z.

Algorytm uczenia można sformułować w następujący sposób:

1. Pokaż obraz wejściowy u i wyznacz wyjście y.
2. Podejmij jedną z poniższych decyzji:
   • jeśli obraz wyjścia jest poprawny, to wróć do punktu 1 i pokaż inny obraz wejściowy u;
   • jeśli sygnał wyjścia jest niepoprawny i równy 0, to dodaj wartość każdego wejścia uⁱ pomnożoną przez pewną liczbę h do wartości odpowiedniego współczynnika wag, w_i;
   • jeśli sygnał wyjścia jest niepoprawny i równy 1, to odejmij wartość każdego wejścia uⁱ pomnożoną przez pewną liczbę h od wartości odpowiedniego współczynnika wag, w_i.
3. Wróć do punktu pierwszego i pokaż inny obraz wejściowy u.

Proces uczenia według tego algorytmu kontynuuje się tak długo, aż w kolejnych iteracjach nie następuje zmiana wektora wag połączeń wstępujących do elementu przetwarzającego. Warto również ograniczyć z góry liczbę iteracji procesu na wypadek ewentualnej jego rozbieżności. Ostatnim problemem jest ustalenie kolejności prezentacji wzorców. Istnieją trzy możliwości:

1. Prezentować dany wzorzec dopóty, dopóki uzyska się stabilny wektor wag i następnie przejść do kolejnego wzorca.
2. Prezentować wzorce cyklicznie zgodnie z ustaloną z góry kolejnością.
3. Do każdej prezentacji losować wzorzec ze zbioru:
   
   
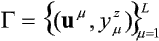
   z prawdopodobieństwem 1/L.

Pierwsza z metod jest niewskazana, ponieważ sieć ucząc się danego wzorca traci zdolność udzielania poprawnych odpowiedzi na wzorce nauczone wcześniej. Drugi wariant unika niedogodności pierwszego, lecz istnieje obawa utraty zbieżności, cyklicznie podawane wzorce mogą bowiem generować cykliczne stany sieci. Preferowany jest zatem wariant trzeci.

Jedną z podstawowych operacji w procesie uczenia elementu perceptronowego jest wyznaczanie współczynników wag w_i. Istnieje kilka metod korekcji wag:

• za pomocą ustalonego kroku wzrostu lub spadku;
• za pomocą kroku proporcjonalnego do różnicy pomiędzy sumą ważoną otrzymaną w sumatorze a oczekiwaną wartością wyjściową; w tym przypadku proces uczenia może być niestabilny;
• za pomocą kombinacji dwóch powyższych metod.

Najprostsza jest metoda ustalonego kroku wzrostu, którą można opisać równaniem:

gdzie:

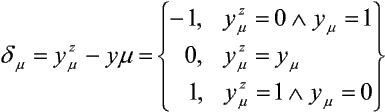
przy czym k oznacza numer kroku algorytmu, w_i(k) - wagę i-tego połączenia na k-tym kroku, u_i^m - i-tą składową m-tego wektora wejściowego u ^m, y_m^z - żądaną odpowiedź na m-ty wektor wejściowy u^m, y_m - aktualną odpowiedź na m-ty wektor wejściowy u^m, h - parametr uczenia. Dla każdego kroku k losuje się odpowiadający mu numer wzorca m. Powyższa zasada nosi nazwę reguły delty. Łatwo zauważyć, że proces uczenia to iteracyjny proces minimalizacji błędów d_m, m = 1, ..., L.

Jedna z interesujących właściwości perceptronu została sformułowana przez Rosenblatta w postaci twierdzenia: jeżeli tylko istnieje taki wektor wag w, przy pomocy którego element perceptronowy odwzorowuje w sposób poprawny zbiór wzorcowych wektorów wejściowych íu^m ý na odpowiadający mu zbiór wartości wyjściowych íy_m^zý, to istnieje metoda uczenia tego elementu gwarantująca zbieżność do wektora w.

W roku 1969 Minsky i Papert zauważyli, że wiele interesujących funkcji nie może być modelowanych przez perceptron prosty, gdyż nie jest spełniony warunek istnienia wektora wag w z twierdzenia Rosenblatta.

Rozważmy element o m wejściach i progu aktywacji q:

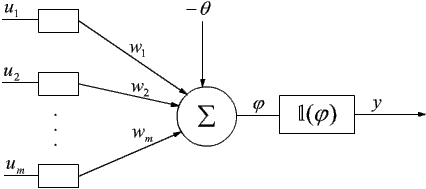
Odpowiedź y tego elementu wyraża się wzorem:

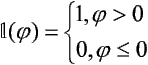
Zatem element perceptronowy dzieli m-wymiarową przestrzeń wektorów wejściowych na dwie półprzestrzenie rozdzielone (m-1)-wymiarową hiperpłaszczyzną o równaniu:

Dla wektorów wejściowych z jednej półprzestrzeni element jest aktywny (y=1), dla drugiej - nie (y=0). Owa hiperpłaszczyzna nosi nazwę granicy decyzyjnej.

Applet pozwalający zaobserwować przebieg granicy decyzyjnej perceptronu prostego oraz wyjaśnienie problemów związanych z próbą zamodelowania za jego pomocą funkcji XOR opisano w części "dla ciekawskich".

Perceptron wielowarstwowy

Ograniczenie liniowej separowalności perceptronu prostego można usunąć poprzez wprowadzenie warstw ukrytych. Oto struktura perceptronu wielowarstwowego:

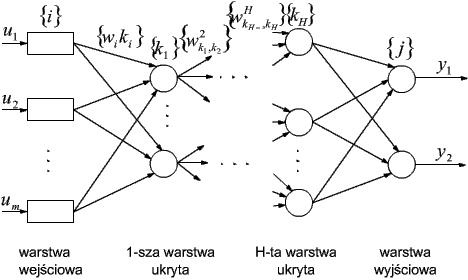
przy czym i = 1, 2, ..., m; m - liczba elementów w warstwie wejściowej; j = 1, 2, ..., n; n - liczba elementów w warstwie wyjściowej; h = 1, 2, ..., H; H - liczba warstw ukrytych; k_h - 1, 2, ..., K_H; K_H - liczba elementów w h-tej warstwie ukrytej; w^h_{kh-1, kh} - waga połączenia pomiędzy elementami k_h-1-tym oraz k_h-tym odpowiednio w warstwach (h-1)-szej i h-tej.

Korzystając z braku połączeń pomiędzy elementami wyjściowymi y_j, j = 1, 2, ..., n, podobnie jak w przypadku perceptronu prostego, rozważymy przypadek sieci z jednym wyjściem:

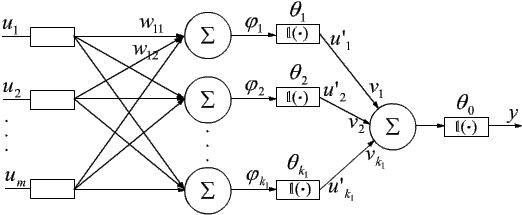
Jest to perceptron dwuwarstwowy opisany następująco:

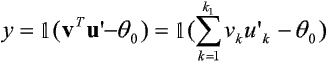
oraz:

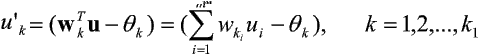
przy czym q₀, q₁, ..., q_k1 są progami bloków aktywacji elementów sieci (0 odpowiada elementowi wyjściowemu, a 1, ..., k₁ - elementom warstwy ukrytej).

Każdy element warstwy ukrytej, podobnie jak opisany wcześniej pojedynczy element perceptronowy, dzieli przestrzeń stanów wejściowych na dwie półprzestrzenie rozdzielone hiperpłaszczyzną o równaniu:

Dla wszystkich stanów z jednej półprzestrzeni dany element jest aktywny, dla stanów z drugiej - nie. Element wyjściowy, działając zgodnie ze wzorem:

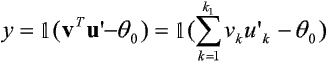
dzieli przestrzeń wektorów wejściowych u na dwie podprzestrzenie uzyskane w wyniku kombinacji iloczynów i sum mnogościowych zbiorów stanów aktywnych poszczególnych elementów warstwy ukrytej. Ponieważ w przypadku perceptronu jednowarstwowego są to półprzestrzenie, jedna z podprzestrzeni stanów aktywności elementu wyjściowego musi być zbiorem wielościennym wypukłym. Wartości wag v połączeń wstępujących do elementu wyjściowego i jego próg q₀ decydują, które z określonych w warstwie ukrytej hiperpłaszczyzn decyzyjnych ograniczać będą utworzony zbiór wypukły i jaka będzie aktywność wyjściowa dla stanów wewnątrz tego zbioru: y = 0, czy też y = 1.

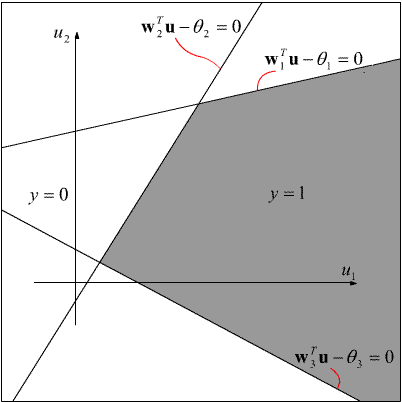
Wynika stąd, że jeśli jeden z dwóch zbiorów wzorcowych wektorów wejściowych odpowiadających wartościom funkcji aktywacji 0 i 1 zawiera się w zbiorze wypukłym, to dane zagadnienie może być rozwiązane przez perceptron dwuwarstwowy. Oto ilustracja zagadnienia realizowanego przez perceptron dwuwarstwowy na płaszczyźnie (czerwone linie wskazują proste opisywane przez dane równanie):

Korzystając z własności perceptronu wielowarstwowego rozwiążmy z jego pomocą problem XOR. Oto odpowiednio schemat sieci i realizowany przez nią podział wektorów wejściowych:

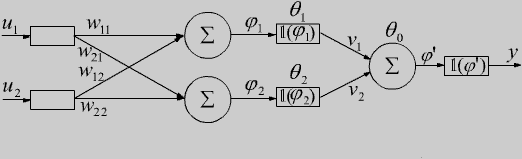
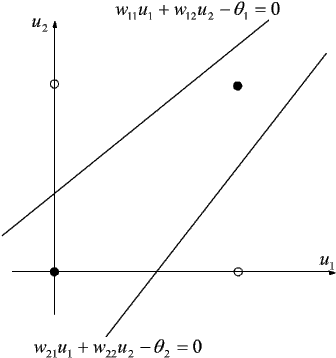
Dalszym stadium rozbudowy omawianej sieci jest perceptron trójwarstwowy, tzn. sieć z dwiema warstwami ukrytymi. Preceptron o takiej strukturze może realizować dowolne odwzorowania przestrzeni stanów wejściowych w przestrzeń stanów wyjściowych. Innymi słowy, perceptron trójwarstwowy gwarantuje istnienie układu wag sieci realizującej poprawnie dowolne odwzorowanie zbioru wzorcowych wektorów wejściowych íu^m ý na odpowiadający mu zbiór oczekiwanych wektorów wyjściowych íy_m^zý. Każdy z elementów pierwszej warstwy ukrytej dzieli, podobnie jak elementy wyjściowe w perceptronie prostym, przestrzeń stanów wejściowych na dwie półprzestrzenie rozdzielona pewną hiperpłaszczyzną decyzyjną. Następnie każdy z elementów drugiej warstwy, podobnie jak elementy wyjściowe w perceptronie dwuwarstwowym, dokonuje pewnej transformacji mnogościowej półprzestrzeni z warstwy pierwszej, dzieląc przestrzeń stanów wejściowych na dwie podprzestrzenie, z których jedną stanowi zbiór wielościenny wypukły. Następnie każdy z elementów warstwy wyjściowej dokonuje transformacji mnogościowej powyższych zbiorów wypukłych, w wyniku której można uzyskać zbiór o dowolnej postaci. Jedynym ograniczeniem jest dostatecznie duża liczba elementów przetwarzających w sieci i połączeń między nimi.