Matematyczny model neuronu

Witam w części "dla fachowców"! Z oczywistych przyczyn pewne zawarte tu informacje będą powtórzeniem fragmentów pierwszej części, choć tam, gdzie nie jest to konieczne, staram się tego unikać. Jeśli zatem nie przeczytałeś części "dla ciekawskich", proszę - wróć do niej i chociaż ją przejrzyj. Na pewno Ci to nie zaszkodzi, a być może pomoże. Jeśli natomiast zaznajomiłeś się z częścią "dla ciekawskich"", przejdź do następnego akapitu.

Strukturę biologicznego neuronu pamiętasz z pierwszej części wykładów. Sztuczny neuron można zaś rozpatrywać jako specyficzny przetwornik sygnałów działający według następującej zasady. Na wejście przetwornika podawane są sygnały wejściowe, które następnie są mnożone przez odpowiednie współczynniki wag (odpowiadające "sile" połączeń synaptycznych w biologicznym neuronie). "Ważone" sygnały wejściowe są następnie sumowane i na tej podstawie wyznacza się aktywność neuronu. Oto schemat sztucznego neuronu:

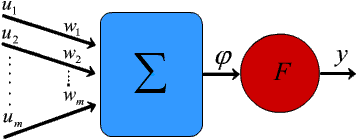
Jak widać na rysunku, model sztucznego neuronu składa się z dwóch bloków: bloku sumowania S i bloku aktywacji F. W pewnym przybliżeniu blok sumowania odpowiada biologicznemu ciału komórki, w której realizowane jest algebraiczne sumowanie ważonych sygnałów wejściowych, oraz generowany jest sygnał wyjściowy j, który może być traktowany jako potencjał membranowy komórki.

Potencjał membranowy możemy wyliczyć ze wzoru:

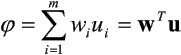
We wzorze tym w jest wektorem współczynników wag, u - wektorem sygnałów wejściowych, (.)^T - operatorem transponowania wektora lub macierzy, m - liczbą wejść neuronu.

Sygnał j poddawany jest przetwarzaniu przez blok aktywacji F, który w zależności od potrzeb może być opisany różnymi funkcjami. Może to być np. prosta funkcja liniowa - wówczas sygnał wyjściowy y ma postać:

k jest zadanym współczynnikiem.

Sieci budowane z wykorzystaniem neuronów o wyjściach opisanych tą zależnością nazywamy sieciami liniowymi. W literaturze sieci takie nazywane są także sieciami Madaline, a tworzące je neurony nazywa się odpowiednio Adaline. Są to najprostsze ze znanych sieci, które znalazły praktyczne zastosowanie.

Innym typem funkcji opisującej blok aktywacji może być funkcja skoku jednostkowego. W tym przypadku sygnał wyjściowy jest równy:

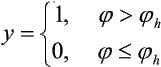
j_h jest zadaną stałą wartością progową.

Funkcjami, które w dokładniejszy sposób opisuję nieliniową charakterystykę przejścia neuronu biologicznego, są funkcje sigmoidalne, opisane wzorem:

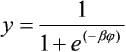
gdzie b jest zadanym parametrem, oraz funkcje tangensoidalne:

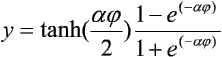
gdzie a jest zadanym parametrem, a tanh(.) - funkcją tangens hiperboliczny.

Należy zwrócić uwagę na następujące zależności dla funkcji sigmoidalnej:

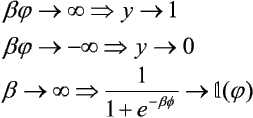
gdzie jest funkcją Heaviside'a:

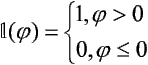
Dla funkcji tangensoidalnej mamy odpowiednio:

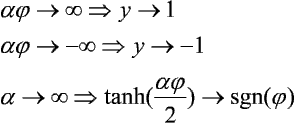
przy czym sgn(>) oznacza funkcję signum, czyli:

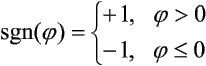
Wykresy funkcji sigmoidalnych i tangensoidalnych mają kształt zbliżony do litery S, a funkcja tangensoidalna jest ponadto symetryczna względem początku układu współrzędnych. Szereg zalet wynikających ze stosowania nieliniowych funkcji tego typu będzie przedstawiony przy okazji omawiania algorytmów uczenia sieci opartych na gradientowych metodach optymalizacji.

Należy dodać, że opisane tu wzory nie uwzględniają wielu charakterystyk biologicznych neuronów. Przede wszystkim są to modele statyczne, w których pominięto czasy opóźnień będące efektem działania dynamiki systemu. Nie uwzględnia się tu również efektów synchronizacji lub funkcji modulacji częstotliwości neuronu biologicznego. Pomimo wymienionych ograniczeń sieci budowane z wykorzystaniem takich uproszczonych modeli matematycznych wykazują wiele cech, które są charakterystyczne dla systemów biologicznych.