Uczymy całą sieć

... czytaj ten rozdział bardzo uważnie, gdyż poruszę w nim bodaj najważniejsze zagadnienie dotyczące uczenia sieci neuronowej.

Po uczeniu pojedynczego neuronu spodziewałeś się zapewne, że następnym krokiem będzie sieć jednowarstwowa. Otóż nie. Powód jest prosty: to zbyt łatwe. Zbyt podobne do uczenia jednego neuronu. Jedyna różnica polega na tym, że dla każdego obiektu wejściowego jest więcej niż jedno wyjście (jest ich tyle, ile neuronów w warstwie). Ponadto proces uczenia sieci jednowarstwowej opisałem z grubsza w pierwszym rozdziale o uczeniu sieci. Zatem wystawimy od razu "ciężką artylerię" i zajmiemy się uczeniem sieci wielowarstwowej. Jeśli zaś czujesz, że chciałbyś jeszcze poćwiczyć z sieciami jednowarstwowymi, polecam książkę profesora Ryszarda Tadeusiewicza pod tytułem "Elementarne wprowadzenie do techniki sieci neuronowych z przykładowymi programami" (Akademicka Oficyna Wydawnicza, 1998). Jest to doskonała książka dla początkujących. Nie ukrywam, że zaczerpnąłem z niej kilka pomysłów na programy, lecz są one tak trafne, że niczego lepszego nie da się chyba wymyślić. Drugi zaś sposób na głód doświadczeń to zapoznanie się ze środowiskiem MatLab i jego toolboxem zawierającym wiele przydatnych funkcji dotyczących SSN. Być może w przyszłości dołączę do niniejszych wykładów krótki opis najważniejszych z tych funkcji.

Ale wróćmy do tematu. Sieci wielowarstwowe to przydatne narzędzie. Pamiętasz zapewne, że to dzięki dodaniu do sieci jednej warstwy można rozwiązać na przykład zadanie XOR. Dlaczego zatem w 1979 roku, kiedy to panowie Minsky i Papert udowodnili, że za pomocą sieci jednowarstwowej nie można rozwiązać wielu zadań, sieci neuronowe na kilka lat popadły w niełaskę? Czyżby nie pomyślano wówczas o sieci wielowarstwowej? Owszem, pomyślano. Niestety nikt nie wiedział, jak taką sieć uczyć. Oto, w czym rzecz: kiedy uczysz sieć jednowarstwową, sytuacja jest klarowna. Znasz wartości wejść dla swojej warstwy, znasz wartości wyjść wygenerowane przez nią, oraz wiesz, jakie mają być prawidłowe wartości wyjść. Na tej podstawie obliczasz popełniany przez sieć błąd, zmieniasz wagi, i tak dalej. Dla jasności rysunek:

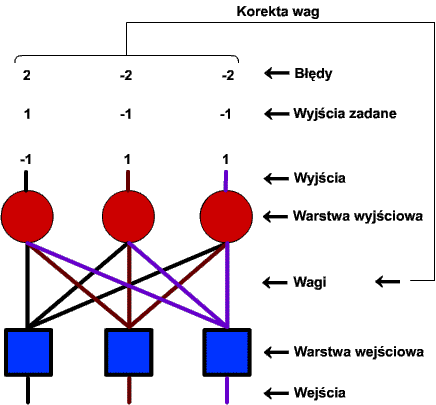
Natomiast w przypadku sieci wielowarstwowej sprawa się komplikuje. Tu z kolei najpierw przedstawię rysunek:

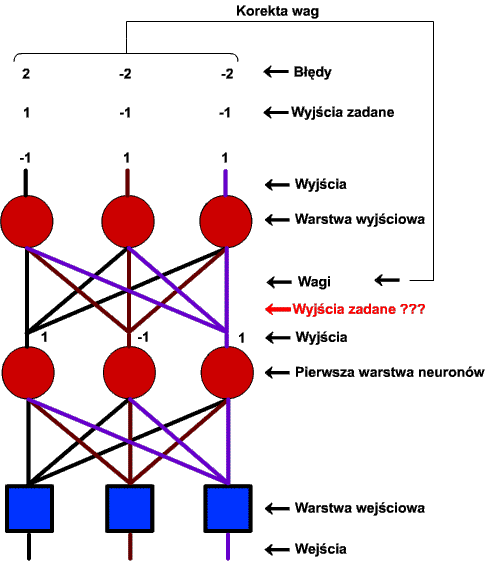
Wiesz już, że aby zmienić wagi danego neuronu, trzeba znać wartość błędu, jaki ów neuron popełnia. Popatrz teraz na ostatnią warstwę sieci wielowarstwowej. Znamy wartości jej wyjść? Znamy. Wiemy, jakie powinny one być po nauczeniu sieci? Wiemy. Możemy obliczyć błąd? Możemy. Jest zatem problem z nauczeniem neuronów ostatniej warstwy? Nie ma. Spójrz jednak na warstwę przedostatnią i zadaj sobie te same pytania. Znamy wartości jej wyjść? Znamy. Nie są one co prawda udostępniane w "zestawie standardowym", gdyż szaremu użytkownikowi sieci do niczego one nie służą, ale my - projektanci SSN - znajdziemy sposób na ich odczytanie. Pytanie kolejne: wiemy, jakie powinny być wartości wyjść przedostatniej warstwy po nauczeniu sieci? Otóż właśnie tego nie wiemy! Znamy docelową odpowiedź całej sieci (w końcu to my ją ustaliliśmy), ale nie wiemy nic o tym, według jakiego algorytmu sieć ustala wagi (a tym samym wyjścia) warstw ukrytych (czyli od pierwszej do przedostatniej włącznie). A skoro nie wiemy, jakie powinny być wartości wyjść warstwy ukrytej, to nie obliczymy też wartości popełnianego przez nią błędu, a zatem nie nauczymy jej niczego sensownego. Nie załamujmy jednak rąk - niezawodna matematyka jak zwykle ratuje nas z opresji. Algorytm uczenia sieci wielowarstwowej został opracowany niezależnie przez trzech naukowców w latach 1974, 1982 i 1986. Został on nazwany algorytmem wstecznej propagacji błędów i wart jest tego, aby poświęcić mu cały następny podpunkt.

Zanim przejdziemy do sedna sprawy, wgłębimy się w zagadnienie kształtu nieliniowej charakterystyki używanej w neuronach. Do tej pory używaliśmy takiej charakterystyki:

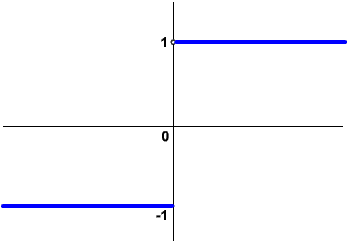
Wzór funkcji opisanej przez tą charakterystykę wygląda tak:

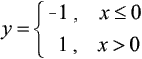
Oznacza to, że dla wartości potencjału membranowego równych lub mniejszych od zera odpowiedź neuronu wynosi: 1, zaś dla potencjału dodatniego: -1. Algorytm wstecznej propagacji błędów (ang. backpropagation) wymaga jednak, aby funkcja aktywacji była ciągła i różniczkowalna, przy czym im prostsza do wyliczenia jest jej pochodna, tym lepiej. Wszystkie te warunki spełnia tak zwana krzywa logistyczna, która wygląda tak:

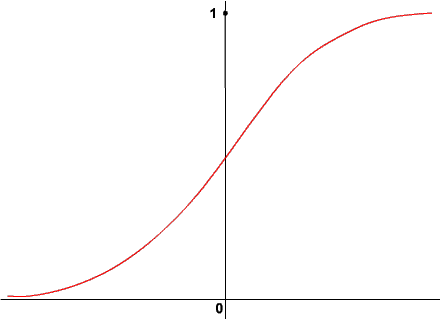
Zauważ, że wartości tej funkcji zawierają się pomiędzy 0 i 1, a nie pomiędzy -1 a 1. Tak też będzie w przedstawionym poniżej applecie. Co nie oznacza, że nie istnieją funkcje opisane przez krzywą logistyczną, których wartości zawierają się między -1 a 1. Istnieją, a jedną z nich, używaną zresztą w SSN, jest tangens hiperboliczny. Kształt krzywej logistycznej może się zmieniać w zależności od parametru beta. Oto przykłady:

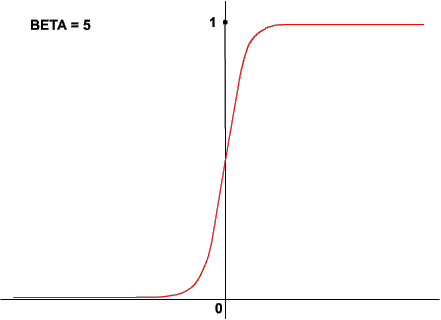
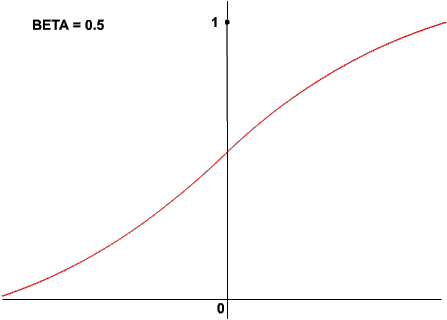
Zauważ, że dla niskich wartości współczynnika beta krzywa przyjmuje kształt bliski prostej, zaś dla wartości wysokich zbliża się do znanej nam funkcji skoku jednostkowego. Dodam jeszcze, że pierwszy z tych trzech wykresów przedstawia funkcję z parametrem beta równym 1.

Krzywa logistyczna bardzo dokładnie odwzorowuje to, co dzieje się w biologicznym neuronie. Tak naprawdę bowiem neuron nie ma zastrzeżonych jedynie dwóch stanów wyjścia: 1 i -1. Pomiędzy nimi jest mnóstwo stanów pośrednich. Jest to swoiste połączenie sieci liniowej z nieliniową. Połączenie o tyle korzystne, że z każdej z owych technik bierze głównie zalety. Posiada zarówno kategoryczność sieci nieliniowej, jak i (dla wartości potencjału membranowego bliskim wartości progowej) ostrożność w ocenie właściwą dla sieci liniowej. W sieci, w której zastosowano skok jednostkowy, wartość wyjścia może się gwałtownie zmienić z -1 na 1. W sieci z krzywą logistyczną zaś ten przeskok nie jest tak gwałtowny - pomiędzy -1 a 1 jest jeszcze -0.7, -0.2, 0.6... i nieskończenie wiele innych liczb.

Oczywiście krzywa logistyczna reaguje na wartość wagi biasu podobnie, jak funkcja skoku jednostkowego:

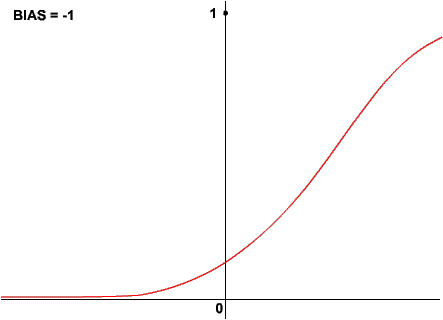
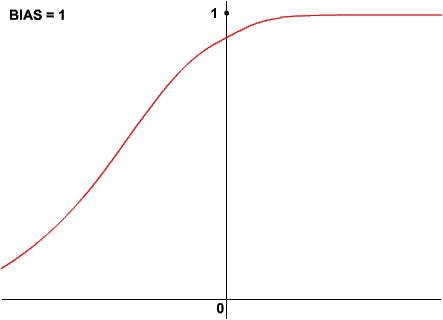
W przykładach, w których prezentowałem parametr beta, bias był równy zero. Masz już dostateczne podstawy do poznania algorytmu backpropagation. Zacznijmy od prostego przykładu działania wielowarstwowej sieci, na razie bez uczenia. Oto schemat dwuwarstwowej sieci posiadającej po dwa neurony w każdej warstwie. Każdy z neuronów ma dwa wejścia oraz bias. Pod spodem objaśnienia:

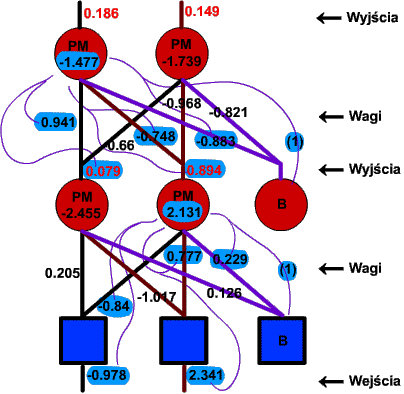
• WEJŚCIA - wartości podawane na wejścia neuronów pierwszej warstwy;
• B - BIAS, który na wejście neuronu zawsze podaje wartość 1; zmienia się tylko jego waga;
• WAGI - wartości wag poszczególnych wejść neuronów; wygenerowane losowo;
• PM - potencjał membranowy; suma ważonych (pomnożonych przez odpowiednie wagi) wejść neuronu;
• WYJŚCIA - odpowiedzi neuronów wyznaczone na podstawie ich potencjałów membranowych według krzywej logistycznej;

Przyjrzyj się dokładnie temu schematowi i upewnij się, że dobrze rozumiesz zasadę działania sieci wielowarstwowej. Za chwilę wyjaśnię, po co ta pstrokacizna, ale wpierw opiszę pokrótce poszczególne etapy działania sieci. Po podaniu danych na wejście dla każdego neuronu obliczany jest potencjał membranowy dla neuronów pierwszej warstwy, czyli suma wejść pomnożonych przez wagi. Jeśli czujesz się w tym, rysunku trochę zagubiony, przyjrzyj się dokładnie wagom - każda z nich dotyka tylko jednego wejścia - właśnie tego, które ma wagę danej wartości. Możesz na kalkulatorze sprawdzić, że wartości potencjałów membranowych rzeczywiście się zgadzają. Następnie wyliczane jest wyjście każdego neuronu pierwszej warstwy. Przypomnij sobie wygląd krzywej logistycznej. Na osi X mamy potencjał membranowy, zaś na osi Y - odpowiedź neuronu. Dla potencjału o wartościach poniżej 2 odpowiedź wynosi około 0, dla potencjału większego niż 2 - około 1, zaś dla potencjału między -2 a 2 odpowiedź zmienia swą wartość między 0 a 1. Obliczone odpowiedzi neuronów pierwszej warstwy trafiają na wejścia neuronów drugiej warstwy. Dla drugiej warstwy wykonuje się następnie te same czynności, co dla pierwszej. Odpowiedzi neuronów drugiej (wyjściowej w tym przypadku) warstwy to odpowiedzi sieci.

Kolorki i kręte kreseczki wprowadziłem, abyś nie miał żadnej szansy się pomylić. Pokazują one, które elementy brały udział w obliczaniu potencjału membranowego prawego neuronu w pierwszej warstwie oraz lewego neuronu warstwy wyjściowej. Do każdego z tych neuronów dochodzą po trzy podwójne kreseczki. Każda kreseczka symbolizuje iloczyn jednego z wejść neuronu oraz odpowiedniej wagi. Wejście biasu nie jest przy tym oznaczone jak inne, zwykłe wejścia, aby widać było, że jest między nim a nimi pewna różnica. W nawiasie obok biasu dla przypomnienia podałem, że wysyła on zawsze sygnał równy 1 (właściwie nie jest to do końca prawda, ale o tym w części "dla fachowców"). I ostatnia sprawa: wejścia pierwszej warstwy są pod neuronami warstwy wejściowej, a wejścia warstwy drugiej - nad warstwą pierwszą. Nie jest to żaden błąd - wejścia pierwszej warstwy (czyli właściwie wejścia sieci) mogłem zaznaczyć zarówno nad, jak i pod warstwą wejściową. Przypominam, że nie wpływa ona wcale na wartość sygnałów wejściowych (nie przetwarza ich), a służy jedynie do rozesłania ich pomiędzy neurony pierwszej warstwy.

Znając odpowiedź ostatniej warstwy, czyli odpowiedź sieci, możemy rozpocząć proces uczenia. Jak pamiętasz, nie możemy bezpośrednio obliczyć błędów popełnianych przez neurony warstw ukrytych. Możemy je jednak oszacować. A dzieje się to z grubsza w następujący sposób: ponieważ wiemy, jakie wartości mają być na wyjściu drugiej warstwy sieci oraz wiemy, jakie są teraz, możemy obliczyć błąd każdego z wyjść. Następnie ów błąd jest przenoszony na wejście neuronu (to właśnie ta czynność powoduje wymóg, żeby funkcja aktywacji była różniczkowalna). Ten błąd na wejściu neuronu drugiej warstwy propagowany jest do warstwy poprzedniej. Na jego podstawie oraz na podstawie wag neuronów drugiej warstwy oblicza się błędy na wyjściach warstwy pierwszej. Te z kolei są przenoszone na ich wejścia. Kiedy już wszystkie neurony sieci mają wyliczone błędy, następuje w całej sieci korekta wag. Wiem, że to zawiłe, ale trudno to wytłumaczyć nie używając języka matematyki. Ambitnym polecam część "dla fachowców", gdzie algorytm jest opisany bez uproszczeń.

Powoli zbliżamy się do końca rozdziału... Przed Tobą applet, który wraz z Tobą poprowadzi proces uczenia wielowarstwowej sieci neuronowej. Dla celów edukacyjnych najlepsza będzie sieć dwuwarstwowa, mająca po dwa neurony w każdej warstwie. Początkowe wartości wag ustalane są losowo. Neurony są oznaczone symbolami (i,j), gdzie:

• i - numer warstwy (0 = wejściowa);
• j - numer neuronu w warstwie (0 = pierwszy z lewej).

Przypominam, że neurony warstwy wejściowej nie robią z sygnałami nic ponad to, że rozdzielają je tak, aby trafiły do każdego neuronu z pierwszej warstwy. Sygnały wejściowe trafiają do neuronów warstwy wejściowej i wychodzą z nich nietknięte. Każdy z neuronów warstwy wejściowej można potraktować jako neuron liniowy z jednym wejściem i wagą równą 1.

Zadanie sieci jest proste. Otóż na wejście neuronów pierwszej warstwy są podawane dwie losowo generowane liczby (oraz bias). Jeśli liczba będąca po lewej stronie (pierwsze z wejść, czyli wyjście neuronu (0,0)) będzie ujemna lub równa zeru, odpowiedź sieci ma być równa: (0,1), czyli na wyjściu neuronu (2,0) ma być 0, zaś na wyjściu neuronu (2,1) - 1. Jeśli zaś lewe wejście (czyli wyjście neuronu (0,0) będzie dodatnie, odpowiedź ma być równa: (1,0). Zauważ przy tym, iż nie ma w taki razie ściśle określonego zbioru możliwych wejść - są tylko określone warunki, jakie wejście musi spełniać. W każdym kroku uczenia na wejściu pojawiają się dwie losowo wybrane wartości, a nauczyciel (czyli algorytm) wymusza na sieci odpowiedź taką, o jakiej właśnie napisałem. Co więcej, po 100 - 300 pokazach (zależy to od "wrodzonych zdolności sieci") sieć zdaje się rozumieć, o co nauczycielowi chodzi! I co - czy to nie jest prawdziwa sztuczna inteligencja?

Ale dość już tych zachwytów... Poniższy applet jest dość skomplikowany w porównaniu z pozostałymi, więc opiszę dokładnie sposób jego obsługi. Na początek wyjaśnienia terminów opisujących poszczególne pola (choć zapewne większość nie jest Ci obca):

• WEJŚCIA - wejścia sieci (losowane w każdym kroku);
• Warstwa wejściowa / ukryta / wyjściowa - słowny opis elementów każdej warstwy, zgodnie z nomenklaturą: (nr warstwy, nr neuronu) (bias ma tylko nr warstwy);
• Wyjście - Wartości wyjść poszczególnych elementów warstwy wejściowej lub pierwszej (zauważ, że warstwa wejściowa ma takie wyjścia, jak i wejścia, a bias ma zawsze wyjście równe 1);
• Wyjście sieci - wyjście ostatniej warstwy, czyli odpowiedź całej sieci;
• Korekty wag - po wykonaniu kroku uczenia algorytm oblicz, o ile zmienić wagi poszczególnych neuronów, ale zanim je zmieni, obliczone korekty pokazuje w tych polach (każde z nich dotyczy wagi znajdującej się bezpośrednio nad nim);
• WAGI - wagi; J
• Błąd wejścia - po obliczeniu błędu na wyjściu danego neuronu oblicza się na jego podstawie błąd na wejściu tegoż neuronu; czyli właśnie Błąd wejścia;
• P. membranowy - potencjał membranowy danego neuronu, którego sposób obliczania powtarzałem do znudzenia;
• Błąd - to właśnie jest ów błąd wyjścia, na podstawie którego oblicza się błąd wejścia;
• Wyjście zadane - takie powinno być wyjście sieci (zauważ, że błąd ostatniej warstwy to różnica między oczekiwanym a rzeczywistym wyjściem sieci);
• Błąd średniokwadratowy... - o tym poniżej;
• Właściwie to o wszystkich pozostałych elementach będzie poniżej.

Początkowo chciałem także zamieścić wyjaśnienie, dlaczego użyłem tylko czterech neuronów, ale chyba nie jest to konieczne - i tak pewnie applet ledwo mieści Ci się w kadrze, zwłaszcza jeśli pracujesz w trybie 800X600.

Teraz opiszę sposób obsługi appletu, a w międzyczasie wyjaśnią się ostatnie wątpliwości co do przeznaczenia reszty przycisków i okienek. Na początku (lub po naciśnięciu przycisku "Nowa sieć") masz tylko wagi (wylosowane) oraz wejścia i zadane dla nich wyjścia. Masz też, co jest oczywiste, wyjścia warstwy wejściowej oraz biasów. Na początku zapewne zechcesz powoli i dokładnie prześledzić, jak to właściwie działa. Do tego służy przycisk "Krok po kroku". Aby wykonać pełny krok uczenia, musisz ten przycisk nacisnąć 16 razy. A oto kolejno wykonywane za jego pomocą operacje:

1. Obliczenie potencjału membranowego neuronu (1,0).
2. Obliczenie potencjału membranowego neuronu (1,1).
3. Obliczenie wyjść neuronów: (1,0) i (1,1).
4. Obliczenie potencjału membranowego neuronu (2,0).
5. Obliczenie potencjału membranowego neuronu (2,1).
6. Obliczenie wyjść neuronów: (2,0) i (2,1).
7. Obliczenie błędu średniokwadratowego obu wyjść i ocena jego wielkości.
8. Obliczenie błędu wyjścia neuronu (2,0).
9. Obliczenie błędu wyjścia neuronu (2,1).
10. Obliczenie błędu wejścia neuronu (2,0).
11. Obliczenie błędu wejścia neuronu (2,1).
12. Obliczenie błędu wyjścia neuronu (1,0).
13. Obliczenie błędu wyjścia neuronu (1,1).
14. Obliczenie błędu wejścia neuronu (1,0).
15. Obliczenie błędu wejścia neuronu (1,1).
16. Obliczenie korekt wag.

Wiesz już, jak się oblicza potencjał membranowy, ale jestem Ci winien wyjaśnienie sposobu ustawienie pól z wartościami wag. Nad każdym neuronem, z którego wychodzą połączenia do neuronów warstwy następnej, są dwie wagi: czerwona i niebieska. Czerwona związana jest z wejściem neuronu po lewej (czyli (x,0)), a niebieska - z wejściem neuronu po prawej (czyli (x,1)). Dla przykładu: waga czerwona nad neuronem (0,0) łączy wyjście tegoż neuronu z wejściem neuronu (1,0), natomiast waga niebieska - z wejściem neuronu (1,1). Dla ułatwienia potencjał membranowy każdego neuronu wypisywany jest w tym samym kolorze, co wagi, które posłużyły do jego obliczenia (nie zapomnij, że do jego obliczenia używa się także wyjść neuronów poprzedniej warstwy).

Wyjście neuronu liczone jest na podstawie jego potencjału membranowego, a zależność między nimi opisuje znana Ci krzywa logistyczna. Znaczy to, że im wyższy potencjał membranowy, tym wyjście jest bliższe jedynki, a im niższy potencjał, tym wyjście jest bliższe zera. Dla potencjału bliskiego zeru wyjście będzie gdzieś w połowie pomiędzy 0 a 1.

Błąd średniokwadratowy wyjść sieci określa, czy odpowiedź sieci mieści się w granicach błędu. Na przykład jeśli sieć miała odpowiedzieć: (1,0), a odpowiedziała: (0.64,0.32), to błąd mieści się w normie. Nie można jednak wtedy osiadać na laurach i przerywać uczenia. Mogło bowiem, zwłaszcza na początku uczenia, "trafić się ślepej kurze ziarno". Dopiero gdy błąd naprawdę zbliży się do zera, można uznać, że sieć jest nauczona, a zapewne i wtedy zdarzy się jej popełnić jakiś błąd. Ucząc sieć trzeba "mierzyć ponad cel, aby trafić do celu" - uczyć sieć perfekcyjnie, dążąc do wymuszenia na niej działania idealnego, aby mogła działać poprawnie.

O błędach wyjścia i wejścia już pisałem. W applecie oznaczyłem je kolorami, odpowiednio: fioletowym i białym. Na podstawie błędów algorytm oblicza korekty wag, które możesz obejrzeć w polach pod wartościami wag. Widzisz zatem, jaka wartość zostanie dodana do aktualnej wagi (lub od niej odjęta). Teraz możesz nacisnąć przycisk "Popraw wagi", aby móc rozpocząć kolejny krok uczenia z nowymi wartościami wag. Jeśli nie chcesz już mozolnie oglądać wszystkich czynności, które składają się na krok uczenia, w dowolnym momencie możesz użyć przycisku "Oblicz korekty". Applet przeskoczy wszystkie pozostałe kroczki aż do obliczenia i wyświetlenia korekt wag.

Zanim błąd zacznie osiągać sensowne wartości, może minąć nawet kilkaset kroków. Aby temu zaradzić, stworzyłem przycisk "10 kroków". Jego przeznaczenie jest chyba oczywiste. Nie daje Ci on jednak pełni szczęścia, gdyż każdorazowo po jego naciśnięciu będziesz musiał nacisnąć także "Popraw wagi". Ale zaufaj mi i uwierz, że tak jest lepiej.

Pole "Suma kroków" opisuje, ile kroków uczenia sieć już wykonała. Współczynnik uczenia już poznałeś, zaś momentum (o którym też już pisałem), to współczynnik "bezwładności" procesu uczenia. Najczęściej ma on wartość pomiędzy 0.7 a 0.9. Taka wartość zapewnia w miarę płynny i spokojny przebieg procesu uczenia sieci. Jeśli pofatygujesz się i przestudiujesz część "dla fachowców", zrozumiesz, na czym polega zasada użycia momentum.

Cóż, to chyba wszystko, co musisz wiedzieć o tym applecie. Nie żałuj czasu i patrz uważnie na ekran, gdyż zrozumienie zasad działania algorytmu wstecznej propagacji błędów jest bodaj najważniejszą rzeczą, jeśli chcesz poznać SSN.

Jeśli masz już dość uczenia sieci, to popatrz, jak uczy się sama.