Samoorganizacja w sieci

Świat zmysłów człowieka i zwierząt jest odwzorowywany geometrycznie w korze mózgowej. Połączenia siatkówki oka z korą wzrokową tworzą mapę retinotopową; ucha z korą słuchową - mapę tonotopową; receptory dotyku skóry tworzą obraz powierzchni ciała w korze somatosensorycznej. Za powstawanie tego typu odwzorowań odpowiada genetyka, a także proces samouczenia się mózgu.

W latach siedemdziesiątych podjęto próbę symulacji tworzenia się mapy retinotopowej. Odpowiednia sieć (na rysunku poniżej) obok jednokierunkowych połączeń pomiędzy elementami wejściowymi i dwuelementową tablicą elementów przetwarzających, zawiera połączenia oboczne pomiędzy elementami przetwarzającymi.

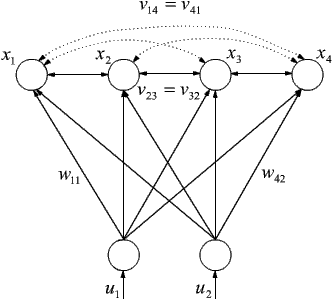
Najsilniejszemu wzbudzeniu podlega element o wektorze wag najbardziej zbliżonym do obrazu wejściowego. Połączenia oboczne wzmacniają wzbudzenia najbliższych sąsiadów, natomiast osłabiają wzbudzenia sąsiadów dalszych, a ich wpływ maleje asymptotycznie do zera wraz z odległością pomiędzy elementami. Ten rodzaj sprzężenia nazywa się modelem kapelusza meksykańskiego:

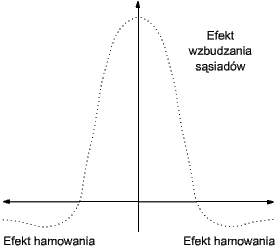
Sieć przedstawiona na pierwszym z dwóch powyższych rysunków nie jest de facto siecią konkurencyjną. Wysokości progów aktywacji zapewniają wzbudzenie kilku elementom wyjściowym. W procesie uczenia stosowano regułę Hebba z każdorazową renormalizacją wag połączeń pomiędzy elementami wejściowymi i wyjściowymi.

W roku 1984 Kohonen zaproponował sieć spełniającą podobną funkcję jak powyższa, opierając się na idei konkurencji. Architektura sieci Kohonena jest uboższa o połączenia oboczne. Aktywacji podlega tylko jeden element przetwarzający - zwycięzca. W odróżnieniu od klasycznych sieci konkurencyjnych modyfikacji wag podlega nie tylko zwycięski element, lecz także elementy jego otoczenia według reguły:

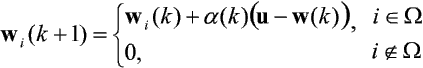
gdzie W oznacza otoczenie elementu zwycięskiego, które może być rozumiane jako zbiór indeksów elementów najbliższych zwycięzcy, np. geometrycznie, w_i jest wektorem wag wstępujących do i-tego elementu przetwarzającego, a u - wektorem wejściowym. Współczynnik uczenia a(k) jest malejącą funkcją czasu. Udoskonaloną formą uczenia jest reguła:

Uczeniu poddaje się tu wszystkie neurony, jednak współczynnik uczenia modelowany jest funkcją z(i,j) odległości i-tego elementu przetwarzającego od elementu zwycięzcy j.

Modyfikacja wag według powyższego wzoru powoduje, że zwycięski element staje się jeszcze bardziej czuły na podawany obraz wejściowy i przy ponownej prezentacji wygenerowany zostanie jeszcze silniejszy sygnał wyjściowy. W przypadku pozostałych elementów, wzmocnienie lub osłabienie wag połączeń jest czynnikiem separującym wektory wejściowe znacznie różniące się od siebie, oraz powodującym aktywację zbliżonych topograficznie elementów wyjściowych w przypadku podobnych wektorów wejściowych. Stąd nazwa sieci: mapa cech Kohonena. Zależność czasowa (iteracyjna) współczynnika uczenia, a zatem i promienia otoczenia elementu zwycięzcy, prowadzi do stopniowego ustalania się mapy topograficznej obrazów wejściowych. W początkowej fazie następuje przyporządkowanie każdej klasie obrazów wejściowych pewnego zbioru elementów warstwy przetwarzającej. Wraz ze zmniejszeniem się wartości współczynnika uczenia zachodzi proces precyzyjnego dopasowywania wag w poszczególnych obszarach warstwy wyjściowej do wejściowych wzorców uczących. Należy dodać, że nie ma określonego teoretycznie sposobu zmniejszania współczynnika uczenia. Kohonen zaleca jego wyznaczanie w sposób eksperymentalny.