Reguły uczenia

Wprowadzenie

Jedną z istotnych niedogodności metod propagacji wstecznej i MRII jako sposobów uczenia sieci neuronowej jest to, że wymagają one "nauczyciela", którego zadaniem jest podawanie dla każdego wektora wejściowego wzorcowego wektora oczekiwanej odpowiedzi sieci. Układ biologiczny, jakim jest mózg, uczy się jednak bez pomocy nauczyciela, rozpoznając świat na podstawie wrażeń zmysłowych baz żadnych bezpośrednich instrukcji.

Wielu badaczy, zwłaszcza tych, którzy posługują się SSN w celu zrozumienia procesów zachodzących w sieciach biologicznych, podjęło się zadania opracowania sieci, która potrafiłaby wykorzystać informacje zawarte w dużym zestawie wzorców, będąc pozbawioną wiedzy a priori o tym, co one reprezentują. Sieć powinna "odkryć" bez zewnętrznej pomocy wzory, cechy, wzajemne zależności, uporządkowanie danych wejściowych, a następnie podać te informacje w odpowiednio zakodowanej postaci na wyjście.

Uczenie "bez nauczyciela", zwane też nienadzorowanym, jest możliwe wówczas, gdy mamy do czynienia z redundancją (nadmiarowością) danych wejściowych. Bez tej cechy obrazów uczących byłoby niemożliwe wyodrębnienie z nich wzorców, czy też rozpoznanie ich cech. Aby sieć mogła pracować bez zakłóceń, powinna istnieć możliwość podziału zbioru obrazów wejściowych na rozłączne klasy, według dobrze określonych cech wspólnych. Sieć powinna być zdolna do zidentyfikowania wspomnianych wspólnych cech w dowolnym prezentowanym wektorze wejściowym.

Reguła Hebba

Opierając się na zasadzie tworzenia się odruchów warunkowych, Hebb wprowadził następującą zasadę. Jeśli aktywny neuron A jest cyklicznie pobudzany przez neuron B, to staje się on jeszcze bardziej czuły na pobudzenie tego neuronu. Jeśli przez x_A i x_B oznaczymy stany aktywacji neuronów A i B, a przez w_AB - wagę ich połączenia synaptycznego, to powyższą regułę można zapisać w postaci następującego równania:

gdzie a oznacza pewną stałą dodatnią, sterującą procesem uczenia.

Reguła Hebba posiada istotną wadę, mianowicie prowadzi do procesu rozbieżnego. Aby to udowodnić, rozważmy liniowy element przetwarzający. Jego stan aktywacji x w chwili k jest równy:

gdzie w(k) oznacza wektor wag wejściowych połączeń synaptycznych elementu, u(k) - wektor wejściowy należący do pewnego zbioru G wektorów uczących, wzięty z tego zbioru zgodnie z rozkładem prawdopodobieństwa, oraz podany na wejście elementu w chwili k-tej.

Zgodnie z ogólną regułą kolejne prezentacje wzorców ze zbioru G zmieniają wektor wag o przyrost DW(k) określony zależnością:

Dalej będziemy zakładać, że elementy ciągu íu(k)ý są niezależne (tzn. wynik losowania wzorca ze zbioru G w danej chwili nie zależy od wyników losowań w innych chwilach). Warunkiem zbieżności procesu uczenia jest zerowanie się (od pewnego momentu) średniej zmiany wag:

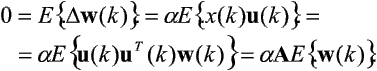
gdzie:

jest macierzą korelacji obrazów wejściowych, a Eí.ý operatorem wartości oczekiwanej.

Zgodnie z definicją macierz A jest macierzą symetryczną. Ponadto można wykazać, że jest dodatnio półokreślona, gdyż:

Wynika stąd, że wszystkie jej wartości własne są rzeczywiste i nieujemne. Wektory własne odpowiadające różnym wartościom własnym są ortogonalne. Z warunku zbieżności procesu uczenia wynika, że potencjalny stan równowagi w_r jest wektorem własnym a₀ macierzy A odpowiadającym zerowej wartości własnej, tzn. w_r = a₀, gdzie Aa₀ = 0. Aby przekonać się, czy stan a₀ jest stanem stabilnym, wystarczy sprawdzić, czy po niewielkim zaburzeniu układ kierujący się regułą Hebba do niego powróci.

Niech wektor w(0) będzie wektorem bliskim a₀, tzn. w(0) = a₀ + e₀, przy czym e(0) jest niewielkim zaburzeniem a₀. Wartość oczekiwana wektora wag w (k + 1)-ym kroku wyraża się zależnością:

Definiując e(k) = w(k) - a₀ otrzymujemy:

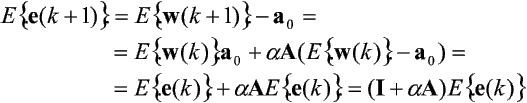
Wynika stąd zależność:

Korzystając z ortogonalności wektorów własnych macierzy A, można ją przekształcić do postaci diagonalnej Z^-1AZ = D, przy czym Z jest macierzą, której kolumny są kolejnymi wektorami własnymi macierzy A, D - macierzą diagonalną, której diagonala zawiera odpowiednie wartości własne macierzy A.

Definiując:

otrzymujemy zależność:

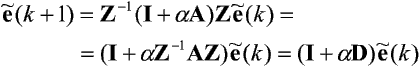
czyli:

Zauważmy, że macierz występująca po prawej stronie powyższego wzoru jest diagonalna. Dla stabilności potrzeba, aby lim_k®Ą Eíe(k)ý = 0 lub równoważnie lim_k®Ą e^~(k) = 0. Stąd i z ostatniej zależności otrzymujemy warunek:

gdzie l_j oznacza j-tą wartość własną macierzy A. Oczywiście warunek ten jest spełniony tylko wtedy, gdy:

Ponieważ jednak a > 0, w konsekwencji otrzymujemy warunek:

Przeczy to jednak dodatniej półokreśloności macierzy korelacji A. Z przeprowadzonego rozumowania wynika więc rozbieżność procesu uczenia według reguły Hebba.

Reguła Oja

Najprostszą metodą zapobiegania nieograniczonemu wzrostowi wartości wektora wag przy korzystaniu z reguły Hebba jest normalizacja tego wektora po każdej iteracji. Wzrasta jednak w ten sposób koszt pracy algorytmu. Można również narzucić ograniczenia dolne (wⁱ_-) i górne (wⁱ₊) na każdą z wag, tzn. w_i Î [wⁱ_-, wⁱ₊]. Oja zaproponował modyfikację reguły Hebba, gwarantującą osiągnięcie stanu stabilnego w przestrzeni wag, w następującej postaci:

Badanie zbieżności tej reguły rozpoczyna się od wyznaczenia potencjalnego stanu równowagi w_r procesu uczenia. Podobnie jak w przypadku reguły Hebba okazuje się, że jest nim jeden z wektorów własnych macierzy korelacji obrazów wejściowych A. Istotnie, załóżmy, że wspomniany wektor wag w_r został zaburzony, tzn. w chwili początkowej mamy do czynienia z wektorem wag w(0) = w_r + e(0), przy czym e(0) ą 0 jest pewnym zaburzeniem początkowym. Na podstawie podanej wyżej równości otrzymujemy zależność:

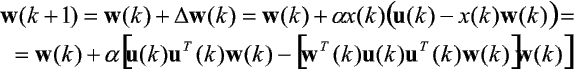
W oparciu o nią otrzymuje się następujące równanie opisujące zmiany w czasie zaburzenia e(k) = w(k) - w_r:

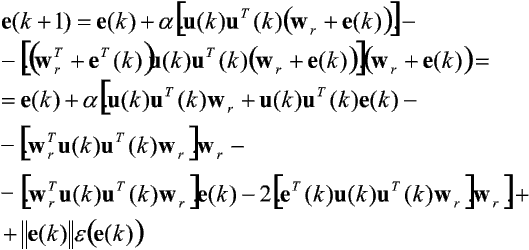
gdzie lim_e®0e(e(k)) = 0.

Zaniedbując w powyższym wyrażeniu ostatni składnik, oznaczający człony wyższego rzędu (innymi słowy - dokonując linearyzacji wokół punktu równowagi w_r), a następnie wyznaczając wartości oczekiwane obu stron, otrzymujemy zależność:

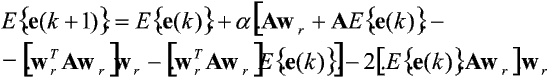
Oczywiście, w stanie równowagi (dla w(0) = w_r) powinna zachodzić równość Eíe(k)ý = 0, k = 1, 2, ... . Po uwzględnieniu jej w powyższym wzorze otrzymujemy następujący związek pozwalający wyznaczyć w_r:

Wynika stąd, że w_r jest wektorem własnym macierzy A odpowiadającym wartości własnej l_p = w_r^TAw_r. Zauważmy ponadto, że wektor ten jest już unormowany, bowiem zachodzi:

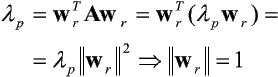
Spróbujmy teraz określić, który z wektorów własnych macierzy A jest stanem równowagi, oraz czy określa on stan równowagi stabilnej procesu uczenia. W dalszych rozważaniach wygodniej będzie używać oznaczenia a_p = w_r, podkreślającego, że w_r jest p-tym z wektorów własnych a₁, ..., a_N macierzy A.

Równanie określające Eíe(k + 1)ý można teraz przepisać w postaci:

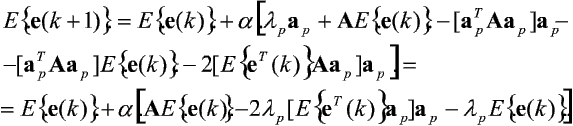
Korzystając z ortogonalności wektorów własnych macierzy A można ją przekształcić do postaci diagonalnej Z^-1AZ = D. Przyjmując, że e^~(k) = Z^-1Eíe(k)ý, otrzymujemy:

Zauważymy, że po diagonalizacji poszczególne równania owego układu są niezależne i mają postać:

gdzie d_ij oznacza deltę Kroneckera.

Wynika stąd, że:

Stabilność procesu oznacza, że musi być spełniony warunek lim_k®Ą Eíe(k)ý = 0, lub równoważnie lim_k®Ą e^~_j(k) = 0, j = 1, ..., N. Stąd i z ostatniej zależności otrzymujemy warunek:

Wynika stąd bezpośrednio, że l_p musi być maksymalną wartością własną macierzy A. Istotnie, w przeciwnym bowiem razie istniałaby inna wartość własna l_q > l_p, jednak wtedy byłoby:

co przeczyłoby poprzedniemu warunkowi. Spełnienie tego warunku dla j = p uzyskuje się poprzez dobór odpowiednio małej wartości współczynnika uczenia a > 0.

W powyższych rozważaniach udowodniono, że wektor wag będący wektorem własnym macierzy A należącym do jej maksymalnej wartości własnej l_max jest, w sensie średnim, stabilnym punktem stałym reguły Oja. Nie jest to dowód zbieżności procesu uczenia zgodnego z tą regułą, który może niekiedy prowadzić do ciągłych fluktuacji bądź zachowań cyklicznych.